Endgames of the World Champions from Fischer to Carlsen
Let endgame expert Dr Karsten Müller show and explain the finesses of the world champions. Although they had different styles each and every one of them played the endgame exceptionally well, so take the opportunity to enjoy and learn from some of the best endgames in the history of chess.
Master Class Vol.1: Bobby Fischer
No other World Champion was more infamous both inside and outside the chess world than Bobby Fischer. On this DVD, a team of experts shows you the winning techniques and strategies employed by the 11th World Champion.
Grandmaster Dorian Rogozenco delves into Fischer’s openings, and retraces the development of his repertoire. What variations did Fischer play, and what sources did he use to arm himself against the best Soviet players? Mihail Marin explains Fischer’s particular style and his special strategic talent in annotated games against Spassky, Taimanov and other greats. Karsten Müller is not just a leading international endgame expert, but also a true Fischer connoisseur.
The match didn’t take place because there was no agreement on the format. Fischer wanted the “10 win system with draw odds.” The first player to score 10 wins would be the victor. But there was a catch: if the score reached 9-9, then Fischer would retain his crown – that is the “draw odds” part of the system. This proposal was rejected. Afterwards, FIDE adopted what I will call the “6 wins system.” The first player to win 6 games would be the champion. There were no draw odds; if the score reached 5-5, they would keep playing. Previously, FIDE had used the “24 game system.” The first player to score 12.5 points or more would be the winner. Fischer would continue his reign if the match were tied at 12-12. Under all three systems, Fischer would have been the heavy favourite — even if I rig a few assumptions in Karpov’s favour.
Why is the model so confident in Fischer’s chances? It’s because of their ratings. Fischer was 2780, just a few points shy of his peak, while Karpov stood at 2705. A 75 point rating gap is not to be lightly dismissed. It’s about the same as the gap between Anand and Carlsen in their matches. Of course, Anand had his chances and the games were not one-sided. But to call Anand vs. Carlsen a 50-50 tossup is just not accurate.
Even worse for Karpov, the match would probably be much longer than either of the Anand-Carlsen duels. And in a longer match, an upset is less likely. That’s because it’s harder for the underdog to consistently beat the odds over many games than it is to beat the odds just a few times. For example, in a large open tournament, a 2200 might score an upset against a GM. But the GM would almost certainly prevail in a 24 game match. Anand’s chances in his 12 game matches with Carlsen were slim. His prospects in a traditional 24 game match would be even worse. That would be like drawing one of the 12 game matches and then winning the other — a pair of unlikely upsets.
Here is how the model works. The ratings give us the expected score. Fischer’s expected score is about 0.6 points per game (see the FIDE handbook for info on the rating system). So if they played a bunch of 10 game matches, we would expect Fischer to win by 6-4 on average.
Master Class Vol.8: Magnus Carlsen
Scarcely any world champion has managed to captivate chess lovers to the extent Carlsen has. The enormously talented Norwegian hasn't been systematically trained within the structures of a major chess-playing nation such as Russia, the Ukraine or China.
𝑒𝑥𝑝𝑒𝑐𝑡𝑒𝑑 𝑠𝑐𝑜𝑟𝑒 = (1)(𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑤𝑖𝑛) + (0.5)(𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑎 𝑑𝑟𝑎𝑤) = 0.6
For now, I will set the probability of a draw at 50%. We will modify that assumption later. Plug that into the equation above, and here’s what you get. In each game, Fischer has a 35% chance of winning, 50% chance of drawing, and 15% chance of losing.
There are three possible formats: the traditional 24 game match, the 10 wins system with draw odds, and the 6 wins system. The best case scenario for Karpov is the 6 wins system. In that format, he is fighting on a level playing field – no draw odds for Fischer. So I ran 10,000 simulations of a match with the 6 wins system. Here is what happened:
Fischer’s chances in 1975 were similar to Carlsen’s chances in 2013.
| Player | Rating | Wins the match % |
|---|---|---|
| Fischer | 2780 | 93.49% |
| Karpov | 2705 | 6.51% |
In the above analysis, I simply assumed that the draw rate was 50%. Even if we change that, Fischer is still the heavy favourite in the simulations:
How Bobby Fischer battled the Sicilian
Fischer liked to play aggressive but basically sound lines against the Sicilian and many of his variations are still very much alive and a good choice for players of all levels.
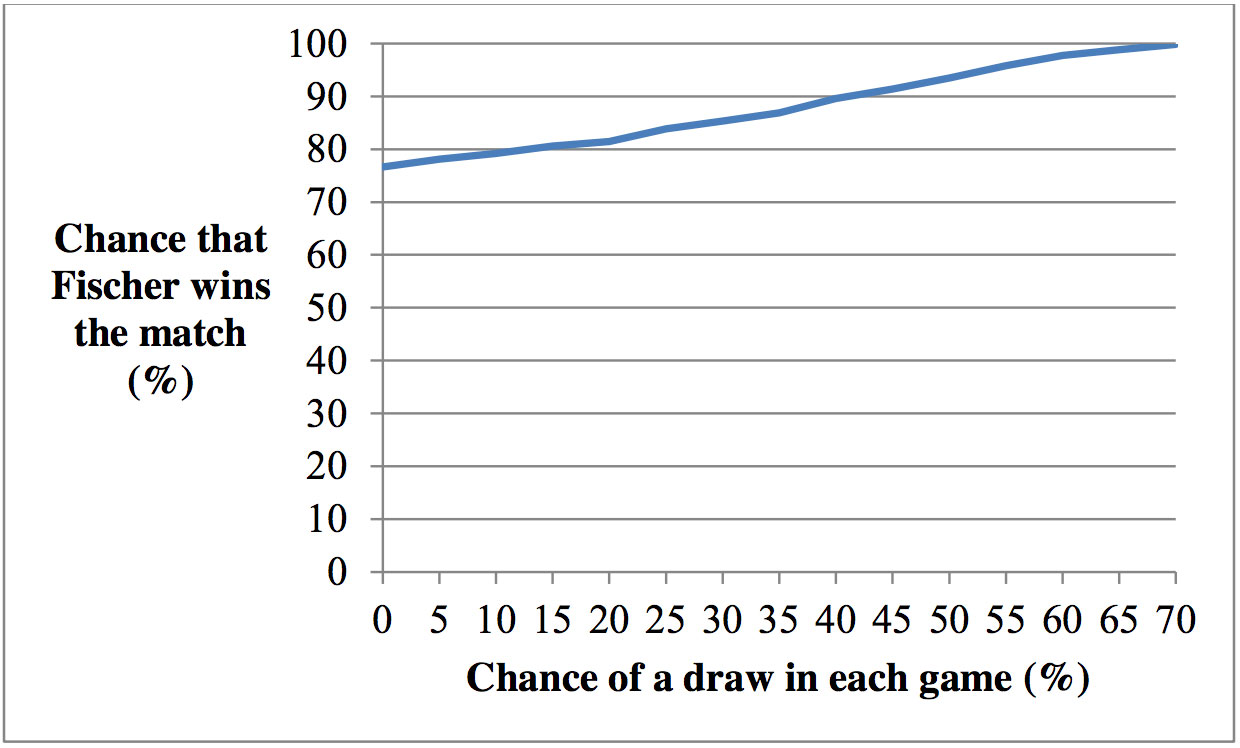
Karpov’s prospects improve when the draw rate is lower — even though draws are not counted in the six wins system. That is not a mistake. If the draw rate falls by 10%, then in each game, Karpov’s chances of winning and Fischer’s chances of winning both rise by 5%. But that causes the ratio of Fischer’s winning chances to Karpov’s winning chances to fall.
Here’s a simple example. We already saw that when the draw rate was 50%, then Fischer had a 35% chance of winning and 15% chance of losing in each game.
𝑅𝑎𝑡𝑖𝑜 𝑜𝑓 𝐹𝑖𝑠𝑐h𝑒𝑟′𝑠 𝑤𝑖𝑛𝑛𝑖𝑛𝑔 𝑐h𝑎𝑛𝑐𝑒𝑠 𝑡𝑜 𝐾𝑎𝑟𝑝𝑜𝑣′𝑠 = 0.35/0.15 = 2.33 𝑤h𝑒𝑛 𝑑𝑟𝑎𝑤 𝑟𝑎𝑡𝑒 𝑖𝑠 0.5
What if the draw rate were 0%? Then since Fischer’s expected score is 0.6, he would have a 60% chance of winning each game and a 40% chance of losing.
𝑅𝑎𝑡𝑖𝑜 𝑜𝑓 𝐹𝑖𝑠𝑐h𝑒𝑟′𝑠 𝑤𝑖𝑛𝑛𝑖𝑛𝑔 𝑐h𝑎𝑛𝑐𝑒𝑠 𝑡𝑜 𝐾𝑎𝑟𝑝𝑜𝑣′𝑠 = 0.6/0.4 = 1.5 𝑤h𝑒𝑛 𝑑𝑟𝑎𝑤 𝑟𝑎𝑡𝑒 𝑖𝑠 0
So when the probability of a draw falls, Karpov’s chances get relatively better in the decisive games.
Possibly. You can see that Karpov was rising rapidly during the early 70s:
Master Class Vol.6: Anatoly Karpov
On this DVD a team of experts looks closely at the secrets of Karpov's games. In more than 7 hours of video, the authors examine four essential aspects of Karpov's superb play.
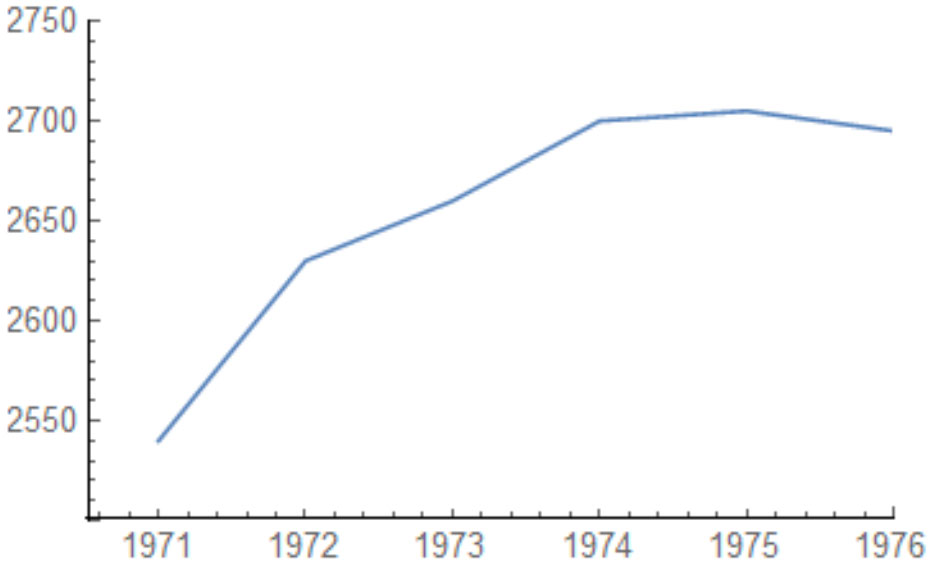
Karpov's rating progression in the 1970s
However, even if we account for this, Fischer remains the clear favourite. And Karpov’s improvement had clearly tapered off by the time he was supposed to face Fischer. I calculated Karpov’s performance rating in 1974 and 1975. He actually underperformed in 1975 and his rating fell to 2695. So I’ll bias the model in Karpov’s favour by focusing his best year. His performance rating was 2726 in 1974.
Let’s say Karpov’s true strength was 2726. He would still be well below Fischer’s 2780. The rating gap would be comparable to that between Carlsen and Giri; they were 60 points apart as of October 2018. Of course you would say that Carlsen would be the favourite in a match with Giri. Only two world championship matches in nearly half a century featured 50+ point upsets. And both of those matches (Kasparov-Kramnik in 2000, Kramnik-Topalov in 2006) were relatively short, meaning that upsets were more likely. Karpov’s chances do improve; Fischer’s expected score shrinks to 57.7%. However, Karpov is definitely still the underdog.
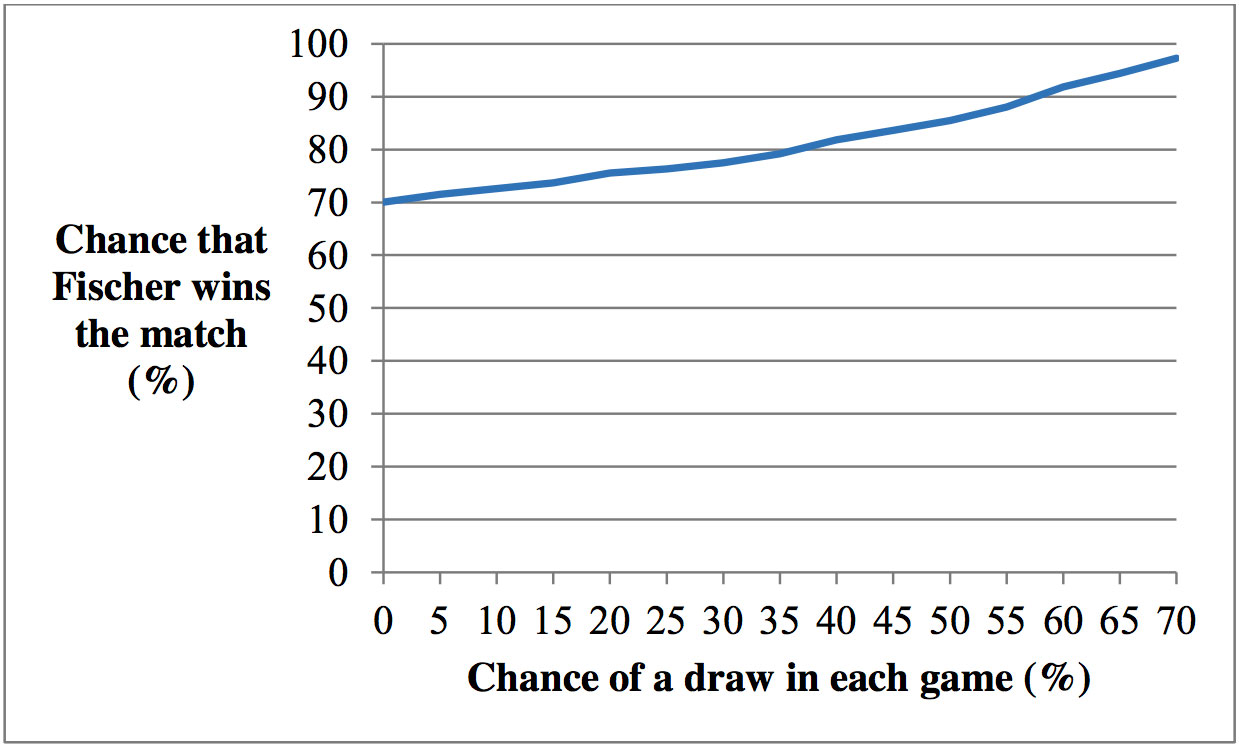
The model implicitly assumes that the games are independent of each other. I tested this assumption many times and never rejected it.
Test #1: If one game is decisive, does that affect the probability of a win or loss in the next game? Perhaps the winner gets a confidence boost and the chance that he would win again would rise. But this is not true, as I demonstrated in an earlier article. Of course decisive games affect the players psychologically, but it does not have any significant effect on the winning and drawing rates.
Test #2: Here is another way to detect a confidence effect. In super tournaments, if you win your previous game, do you outperform your rating in the next game? The answer is no.
Test #3: Suppose that winning your previous game gives you a confidence boost that helps you in the rest of the tournament. If that is true, then results in actual tournaments will be more spread out than my simulations would suggest. My model would have too many players bunched up at 50% and not enough at the extremes. However, a statistical test rejected this argument.
Test #4: Once a player gains a significant lead in the match, he will start playing for a draw. Thus, the draw rate should not be constant in the simulations.
This argument doesn’t apply to the six wins system that I have investigated here. However, it would be plausible if FIDE had insisted on the traditional 24 game match. However, there is no evidence that the draw rate changes once a player takes a 2 point lead. Naturally, the leader is inclined to play safely, but this is balanced by his opponent’s extra motivation to fight for a win.
At the top level, the games really do seem to be independent of each other.
It was a tragedy for chess that the match never took place. However, we can be quite confident that Fischer would have prevailed. It is true that the model does not directly account for factors such as Fischer’s mental health. However, his 2780 rating that was used in the simulations was his actual rating — the rating he attained in spite of his issues. This is not an imaginary problem-free version of Fischer.
Are nerves a factor in a world championship match? Of course they are. But the ratings used in the simulations come from real tournaments and matches in which nerves were also a major factor. Thus, the results in the simulations cannot be easily dismissed.
Karpov’s chances are low even if we twist the model’s assumptions in his favour. Even if we pick a system in which Fischer does not have draw odds and even if Karpov were underrated, Fischer is still the heavy favourite. Fischer’s chances are — at the bare minimum — 70%. I do not know how long Fischer’s reign would have lasted; perhaps Karpov would learn important lessons from their match and come back stronger in 1978. But we can be quite confident about the outcome in 1975.
