

 Jeff Sonas, Chessmetrics, California, USA
Jeff Sonas, Chessmetrics, California, USAIn my recent letter I very clearly stated that my conclusions (regarding a K-factor of 24 versus 10) were based upon extensive analysis I performed in 2002, and I also was careful to ensure there would be a hyperlink to my 2002 ChessBase article describing that analysis. I find it somewhat perplexing that Dr. Nunn took the time to quote an extract from my recent letter, but apparently did not take the time to read through the linked article from 2002. Dr. Nunn asks where the proof is. The proof is very clearly there, in my opinion, if you follow the link and read the article.
Nevertheless I do believe there is room for improvement in my analysis from 2002. I believe that it is extremely important to use the same set of data that FIDE used for the official rating calculations. As GM Krasenkow points out, the impact of the "before 2400" rule could be quite significant, and my set of game data was not necessarily comprehensive for lower-rated or new players. It is quite possible that he is correct. So I would really just repeat what I said before, which is that I think it would be useful to perform the analysis again, using the official dataset from FIDE (if they are interested in providing it to me). I also think it would strengthen the conclusions if the comparison used formulas that were both published prior to when the games were played. Otherwise I could be accused of "training" my formula so it matched only historical data.
I am confident that if we took the official FIDE games from the past ten years (1999-2009), and gave the two rating systems a few years (1999-2002) at the start in order to diverge from each other, and then reviewed the results of games played since the publication of my article (2002-2009), that the Sonas formula (including K-factor of 24) would prove more accurate at predicting the results of those games since 2002 than the existing Elo formula (including K-factor of 10). I even promise to announce the results no matter what…
Nate Solon, Nice, France
I agree with Dr. Nunn in that I don't see the connection between more frequently published rating lists and the K-factor. But, in attacking Sonas's lack of evidence for preferring a higher K-factor, maybe he missed this section of Sonas's report:
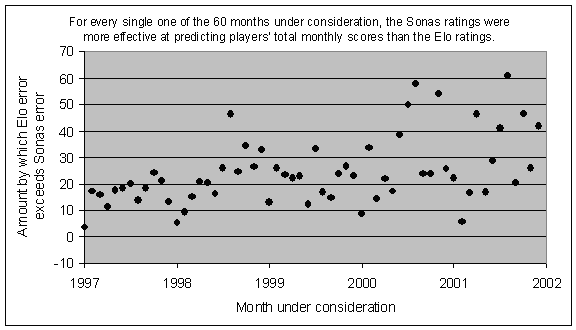
"How can I claim that the Sonas ratings are 'more accurate' or 'more effective at predicting'? I went through each month and used the two sets of ratings to predict the outcome of every game played during that month. Then, at the end of the month, for each player, I added up their predicted score using the Elo ratings, and their predicted score using the Sonas ratings. Each of those rating systems had an 'error' for the player during that month, which was the absolute difference between the player's actual total score and the rating system's predicted total score.
For example, in April 2000 Bu Xiangzhi played 18 classical games, with a +7 score for a total of 12.5 points. Based on his rating and his opponents' ratings in those games, the Elo rating system had predicted a score of 10.25, whereas the Sonas rating system had predicted a score of 11.75. In this case, the Elo error would be 2.25, whereas the Sonas error would be 0.75. By adding up all of the errors, for all players during the month, we can see what the total error was for the Sonas ratings, and also for the Elo ratings. Then we can compare them, and see which rating system was more effective in its predictions of games played during that month. In the last graph, you can see that the Sonas ratings turned out to be more effective than the Elo ratings in every single one of the 60 months from January 1997 to December 2001."
It would be one thing if Nunn questioned Sonas's method or his numbers, but instead he entirely disregards the evidence Sonas already provided (which is considerable and, I think, convincing).
Clearly there are disadvantages to both low and high K-factors. A too-low K would lead to stagnant, unresponsive ratings, whereas a too-high K would lead to wildly variable ratings. The challenge is to find the sweet spot between the two extremes. Sonas says that spot is 24 based on analysis of thousands of rated games over many years. Nunn says it is 10, but doesn't offer a reason why.
On the other hand, the negative reaction of Nunn and other grandmasters is in itself proof that FIDE did a poor job publicizing and explaining this change.
Predictive power versus real strength
As a reaction to the latest considerations from Jeff Sonas and John Nunn, as published by ChessBase, I'd like to offer a some thoughts about the connection between higher Ks and stronger "predictive power". About higher K, GM Nunn wrote the following:
"[...] there seems no particular reason to believe that the rating will more accurately reflect a player’s strength or better predict future results."
My view is that Nunn's mixing two rather different animals in the above:
Note that I also consider "future results" to be a slight misnomer: we're talking about a very near future – in fact only about the results in tournaments played before the player's rating again changes (or is "adjusted"). This is in fact very interesting – it highlights a difference between two partly exclusive goals for a rating system, where it appears that John Nunn and Jeff Sonas want different things.
The basic argument Jeff Sonas has put forward for why his system is "better" than that of FIDE, is that it predicts results better (less discrepancy on average between "expected score" and "actual result"). Of course it can be argued that Sonas' formulas have been fitted to be a best possible match of a subset of results, mostly of players of FM/IM strength and above – and that his "test" and comparison to the FIDE system and their formulas mostly has been against the same kind of data that was used to create Chessmetrics. Also, Sonas has adjusted his system for each new revision of it, after new data have become available and previous data have been "improved".
The above is less important, however.The important thing is to consider why possibly a more dynamic system (higher K and more frequent lists) would predict results better for a player in his next ("immediate", more than "future") event. Is it
Ivanchuk is the perfect example of a player for which a very dynamic system would probably yield clearly stronger predictive power. But does it more accurately describe Ivanchuk's real abilities as a chess player? In my opinion, this again boils down to a couple of reoccuring points:
When people dismiss ratings as being "useless", the reason is usually one of two: Either ratings failed to accurately predict results in an event, or the exact ranking based on ratings is different from what people "feel" is correct, based on their notion of "real/true strength". Often the same people use both arguments. Based on the arguments presented here, it follows that I consider both reasons to rely on slight misconceptions or misunderstandings about what ratings are. The more interesting question, however, is what we want rating numbers to most accurately describe, and possibly if they could be presented in a way that highlighted both their strengths and their limitations better than what the naked number currently does.
A. N. Burumcekci, Istanbul, Turkey
If one studies Mr. Elo's book on the subject, one realizes that Elo system was designed for a pool of players where the weakest and strongest are 3-4 classes apart.
The first error that Fide has made in recent years was to lower the Elo rating threshold from 2200 to 1600 gradually. The only reason for this, as I see it, is to increase revenue from rating fees. When you lower it this much, we will end up having a "1600" rating from country X being much stronger than a rating of "1600" from another country. This is very obvious as players in country X play against each other in a closed pool, and rating changes occur within these players. It does not matter whether these players do nothing to improve themselves other than playing against each other or study books to improve themselves. If they do not play with players from other countries, they will just keep changing rating points within themselves.
How many players between 1600-2200 rating play against players from other countries within 1600-2200? Now compare this number with players with 2200+ ratings playing with players with 2200+ rating from other countries? 2200+ players have far more opportunites to play with foreign 2200+ players.
Therefore the old system with a minimum 2200 rating did a better job of estimating a player's strength than the current system.
The second error to be made is the increase of the K factor. A rating shows a player's past performance; it does not estimate future performance! K factor decides how much importance is given to prior performances.
Let us assume that Kasparov decided to return to chess, and is a shadow of himself. He does not follow theory, he does not prepare for opponents, he relies on his natural talent alone which, for the sake of argument, I assume to be 2500. (I am in no position of making such an assumption; this is just a figure I made up). With a K factor of 10, his rating will fall to 2500 in 85 games within a rating period. If he had a K factor of 25, then he had to play only 34 games in a rating period to lower his rating from 2800 to 2500 in a rating period.
Mr. Elo made the assumption that a player new to the list is an improving player and hence gave a K factor of 25. He assumed that a player with a rating above 2400 will show consistent performances. A player's rating with a K factor of 10 shows that s/he has achieved his/her rating with a lot of tournament performances in his/her bag. If K factor is increased to 25, 30 or whatever, this rating will be published with less number of tournament performances. A rating of 2600, or 2800 or any other figure will be easier to achieve and hence devalue it. We will see some current 2500 players increase their rating to 2600, and then go back to 2500 again. What will this achieve? If this player is invited when the rating is 2600, and his rating drops back to 2500 before the tournament, then the organiser will have a lesser category tournament. Therefore the organiser will try to invite a player that has a 2600 rating, not in one list, but preferably in 3-4 or more lists. This way the tournament organiser will make sure that the player will show a performance of 2600 in the tournament. This is the current situation we have! Increasing the K factor will make ratings less informative of a player's true strength.
Decreasing the rating period from 6 months to 2 months will make it harder for a player to increase or decrease his/her rating. This will make a player harder to get to 2600 or any other line. It will also protect players with bad performance; they will lose less ratings.
This is in opposition of the belief that increasing the K value will award players with recent performances. Increasing the K value definitely will reward recent performances much better than previous performances; but increasing the rating list published within a year will make that rise to the top, or fall from the top harder. These two cannot go in hand to hand.
Elo system served us well in the past. The administrative interference to lower the rating has made it perform worse. The second interference proposed (increasing the K factor) will make it less solid as a system of informing a player's strength. We may need to improve the Elo system, but these proposals just be made statisticians and rating administrators; not by some administrators or players. Rating regulation 12.3 is explicit in this. Also 13.1 should be worded "extensive" rather than "sufficient" if we need a scientific system intact.