ChessBase 17 - Mega package - Edition 2024
It is the program of choice for anyone who loves the game and wants to know more about it. Start your personal success story with ChessBase and enjoy the game even more.
In February 2003, a nine-year-old boy named Xaver caused a minor sensation on German TV. It was on the show "Wetten dass...?", which translates approximately to "Wanna bet...?" The format is that a series of candidates propose to be able to do impossible feats, live and in front of the camera. For instance uncork a bottle of wine using a corkscrew attached to the landing gear of a helicopter. The boy on the show bet that he could complete a "Knight's Tour" of the chessboard, completely in his head, starting from any square on the board.
A "Knight's Tour" is a sequence of 64 knight moves executed in such a way that each square of the board is visited exactly once. The young lad was blindfolded and a starting square was called out to him. Without much thought he dictated a sequence of 64 squares that comprised a perfect knight tour.
The reaction to this feat in Germany was overwhelming. Newspapers were full of it, people discussed it on trains and buses, in offices and schools, and we at ChessBase received dozens of calls urging us to tell the story on our news page. This we did at the time, but with some misgiving: was it right to join the general speculation that we might have encountered a future chess world champion, or at least been witness to a prodigious feat of pure genius? Or should we look deeper, even if our results would detract from a moment of glory for a nine-year-old child? Should we tell our chess savvy public that the feat on the TV show was not quite as impressive as it looked?
The "Knight's Tour" of the chessboard was first proposed (solved) in a ninth century Arabic manuscript by Abu Zakariya Yahya ben Ibrahim al-Hakim. The author give two tours, one by Ali C. Mani, an otherwise unknown chess player, and the other by al-Adli ar-Rumi, who flourished around 840 and is known to have written a book on Shatranj (the form of chess then popular).
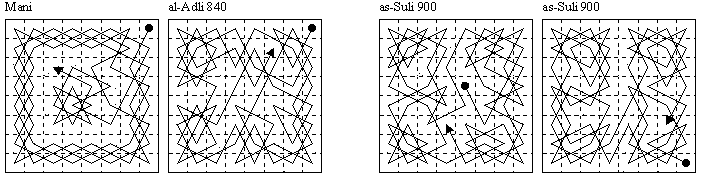
A "closed tour" is one in which the square at the end of a Knight's Tour is a knight move away from the first square, as in the second example above. The master of Shatranj as-Suli, who based his works on those of al-Adli (which he criticised), published the two closed tours given above on the right. The first example shows perfect axial symmetry on the left half-board, the second is composed of two quasi-symmetrical half-board tours.
The first comprehensive mathematical analysis of the Knight's Tour was presented by the eighteenth century mathematician Leonhard Euler (1707–1783) to the Academy of Sciences at Berlin in 1759. The Academy had proposed a prize of 4,000 Francs for the best memoir on the problem, but it was never awarded, probably since Euler was at that time Director of Mathematics at the Berlin Academy and presumably ineligible.
Incidentally the number of possible knight's tours on an 8x8 board is surprisingly large — estimates range between 13 and 33 trillion. And much more on bigger boards. Here, for curiosity’s sake, is a Knight Tour on a 130x130 board.
If you want to learn a closed knight's tour by heart pick one of the following by Leonhard Euler. Learning a closed tour had the important advantage of allowing you to start from any square on the board and complete the tour from there. It is as easy as reciting the numbers from 1–64 starting from some random number and cycling to 1 after reaching 64.
Let us return to our nine-year-old boy on the TV show. As mentioned in the introduction to this article, Xaver was able to complete a Knight's Tour blindfolded and from any starting square given to him by the host of the show. Exactly how prodigious was this feat? How deeply must we be impressed?
Learn to master the right exchange! Let the German WGM Elisabeth Pähtz show you how to gain a strategic winning position by exchanging pieces of equal value or to safely convert material advantage into a win.
In order to test the effort involved in learning a Knight's Tour I asked a guest who was visiting over the weekend when the TV show was aired: Elizabeth Paehtz, at the time the women's under 18 world champion. "I used to be able to do the Knight's Tour when I was a child," she told us, "but I have forgotten how it went." So we asked her to try to learn it again.
Using a Knight's Tour of her choice Elli started learning it by heart. It was not as easy as she thought! With some effort she was able to master a tour in 40 minutes. It must be mentioned that the poor thing was in considerable pain, having had two wisdom teeth extracted a few days previously. So there was some problem with motivation.
How to play the Sicilian Defence!
The continuous stream of new ideas in the Sicilian makes 1..c5 the most popular answer to 1.e4. On this DVD I do give an introduction to the most important Sicilian systems.
How about someone who is not a very strong chess player? Thomas Friedel, 20, gave up competitive chess when he was 14 and became a full-blooded programmer. How would an algorithmic mind fare with the task? With all his teeth intact, after twelve minutes studying the diagram Tommy announced that he could do it. And indeed, with Elli checking the moves he completed a Knight's Tour flawlessly on an empty chessboard. He could only do it starting from one particular square, but wagered that with half an hour of additional practice he could pick it up at any point in the closed circuit. Maybe an hour to do it reliably, dictating the squares rapidly, with a blindfold covering his eyes.
Sorry, Xaver, for demystifying your great performance. And sorry to everybody for being such spoilsport. I can only give you the following advice: pick a closed Knight's Tour from the Euler group above and invest an hour or two learning it. You can also download a Knight's Tour app to practise. After you have mastered the task prepare for your moment of glory. If it doesn't get you on big TV show, it at least makes for a great party trick.
When writing this article I remembered one of the most remarkable mental performances I have ever witnessed. It happened many years ago, at a U.S. chess club, where a master was giving a demonstration of his extraordinary abilities. At one stage he asked for a helper from the audience, and I was pushed and poked by my friends to take to the stage. There the master gave me a block of sticky notes and asked me to write down names, words and numbers dictated at random by the audience. Each was stuck on a big demo chessboard, starting from the square a8 and working sequentially to h1.
The audience called out a variety of words: names of cities, family members, phone numbers, abstract expressions. It went something like this: Dayton, Margaret-Lee Farrow, Pride before a fall, 212-783-4529, My dad's dog Skippy. While it was being done the master sat on his chair, listening to the audience, chatting with them. He was completely relaxed and not making any visible effort to memorise the notes.
After all the squares had been covered the master was blindfolded. He then asked someone in the audience to name a square on the chessboard. He immediately quoted the text that was on that square, and then proceeded to call out other texts on the sticky notes (which I located and removed from the demo board). The order in which he did this resulted in a perfect Knight's Tour. I believe he got one or two words slightly wrong, on the lines of Margaret-Mae Farrow instead of Margaret-Lee. All the numbers were perfect.
Now that is a truly remarkable feat. We were all deeply impressed, not the least because the master was approaching ninety years in age! He was George Koltanowski, one of the greatest mental acrobats the world has ever seen.
George Koltanowski, 1903-2000, picture originally in the San Francisco Chronicle 2000
All you could ever want to know about the Knight's Tour can be found here and here (and plenty of other locations).
