ChessBase 17 - Mega package - Edition 2024
It is the program of choice for anyone who loves the game and wants to know more about it. Start your personal success story with ChessBase and enjoy the game even more.
There are a few dedicated fans of longevity, those who celebrate chess masters who reach great ages - the legendary “match of the 200 years” between Aaron Schwartzman (104, then 101) and the young Francisco Benkö (99) being one of the highlights where such celebrations reached a further chess public. Zoltan Sarósy (110) might have been the oldest such master. On the female side, several participants in the 1939 World Chess Championship - Catharina Roodzant (103), Berna Carrasco (98) - reached over 90 years, with Mona Karff (89) just barely missing it. Last year, another such hero of both chess and longevity passed away: Richard Kenneth Guy, the probably most important amateur mathematician. Richard Kenneth Guy, who survived half of a World War, a pandemic, another World War, and three quarters of a century later at the age of 103 fell victim of another pandemic that likely had its origins in September or October 2019 and as of writing this article is still ongoing.
"Math is beauty, can't you see? It's the art of numeracy!" is asked by the soundtrack of an incremental game. When I started a draft about Guy last year, I wrote this about the both mathematicians:
Richard Kenneth Guy (30 September 1916 - 9 March 2020) passed away only shortly before John Conway (26 December 1937 - 11 April 2020), the inventor of the “Game of Life”, a mathematical/geomatrical simulation that sets strict rules for patterns on a grid (similar to a chessboard but infinite in length and width). Each square can either have or have not a “living cell”, and if a certain number of living cells are next to a square, it will contain a living cell in the next move. After setting up an initial pattern, the game plays itself with the predetermined moves.
Richard Guy was one of the first to study it with Conway’s rules, finding a self-sustaining “moving” geometrical pattern (or rather two alternating patterns that shift) known as the “glider” - obviously this was "computed" by hand, as computers at that time weren't advanced enough to run this game, which by the way is Turing complete.
As every state of the board after the initial first one is determined, the interest in this game is not in actively playing it (there is no user input for the gameplay) but rather in seeing how patterns play out, and in finding patterns that transmit information to other patterns. Complex “organisms” can even create gliders and other objects that are self-sustainable. The dimensions of such patterns reach far beyond anything comprehensible by a typical human mind, as evidenced by even recent discoveries.
The forums for the “Game of Life” are very active, and there are new discoveries that are ranked each year while currently the “Pattern of the Decade” (2010-2019) is voted for. For example, an oscillating pattern that repeats every 23 turns named “David Hilbert” (in reference to David Hilbert’s 23 problems) by Luka Okanishi, based on a partial result by Aidan F. Pierce, was voted as the best discovery of 2019. With not too much imagination, we might even see a (Hilbert’s?) face in the pattern...
After I had written that draft, I noticed that I would be unable to do any justice to the "Game of Life", so we will just not talk about it. I mean, who are we? People who look at a grid of cells and try to figure out where some pieces on it will go in 5, 10, 20 or even 50 moves. Maybe not so different from the "Game of Life" enthusiasts after all, but if you would try to convey the beauty of chess to someone who has no interest in geometry... so let us just agree that the both worlds are similar but different.
I saw a beautiful video on Youtube last month that talked about a game named "Hackenbush". But then something happened, the video that was about the game had an excellent introduction to "surreal numbers". Endgame study composer Hauke Reddmann, an amateur mathematician himself who proofread my article this month, sent me his thoughts, improving on my original draft I had here:
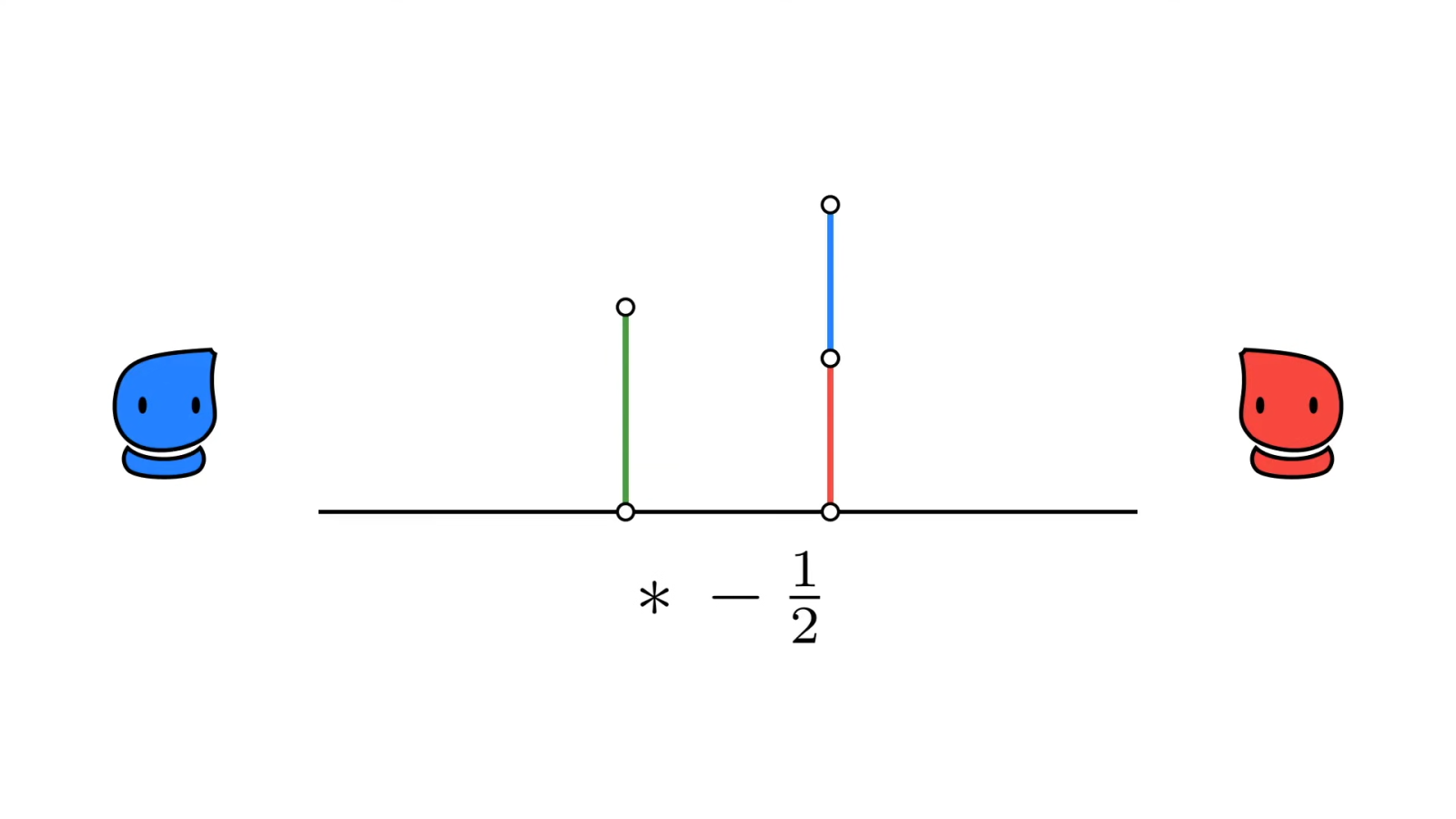
"From school you surely know real numbers. And from USENET (sci.math) you might know people who would kill for their opinion that 0.999999... and 1 are two different numbers. Now, math is a game, and if you don't play by the rules, mathematicians simply won't play with you.
The rules of real numbers require 0.999999...=1, and that any two real numbers except 0 are "comparable" - whereas there are infinitely many real numbers between 0 and 1, there are no "infinitely small" numbers like the suggested difference between 0.999999... and 1. But as a mathematician, you can invent a new rule system with the stroke of a pencil, as long as it is self-consistent. Surreal numbers are such a system.
They can be infinitely small, and there are even a lot of different kinds of smallness (for example the number called "arrow up" is sort of the advantage of putting your opponent in zugzwang), so you now have more than one number that might be called 0.999999..., and 1 still has no "left neighbor"!
Conway invented the surreal numbers just by declaring a few recursive rules for an ordered pair of two number sets, and together with Guy and Berlekamp they sorted out all the beautiful consequences of this construction and wrote, as you latest found out at the end of the video, the book... (etc.)"
At the end of the lesson, we find out that the video actually was not only about teaching surreal numbers, but about a book: "Winning Ways for Your Mathematical Plays", a definitive work about game theory by Elwyn R. Berlekamp, John H. Conway and Richard K. Guy. The latter two authors also wrote "The Book of Numbers", and Conway alone "On Numbers and Games".
I instantly recognized two of the three names, Berlekamp being a name I probably had heard before but forgotten, included one of Guy's studies in the article and decided to write more about him Conway later...
As an interesting fact, the Canadian Mathematical Society, apparently together with the University of Calgary's Department of Mathematics and Science, published an original article from Berlekamp and Guy in their October 2020 issue of Crux Mathematicorum. We take some information from the tribute by Bill Sands there, and also leave it as an exercise for the reader to figure out what is special about the sequence 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17 which was found by Bernardo Recaman Santos, of Colombia, and published as one of the solutions of the 2000 World Puzzle Championship. The solution is at the end of the article. The entire archive of the magazine is available for free on the official website.
So to get it out of the way, let us repeat Richard Guy's least important achievement first, which I mentioned last month: 238 endgame studies (versions included), 230 of them between 1936 and 1954. Together with John Roycroft and Hugh Blandford, he invented the "GBR Code", Guy-Blandford-Roycroft Code, to mark material used in endgame studies. It has certain limitations, but its extended version can be used to completely give positions of endgame studies that have no more than two of the same piece (pawns excluded) per side.
According to Roycroft's "The Chess Endgame Study" ("Test Tube Chess"), Guy worked as editor for endgame studies for the British Chess Magazine from 1947 to 1951. He was succeeded by Hugh Blandford...
Bill Sands writes that Richard Guy coined the term “n choose k” for its binomial symbol. Apart from the above-mentioned "Winning Ways", where Guy contributed to two volumes, he also wrote many other books, including about "Unsolved Problems in Geometry" (co-authored with Croft and Falconer), "Unsolved Problems in Number Theory".
On the website of the University of Calgary, we read about Guy, who had arrived there in 1965 and supported the University a year later when it started anew, together with his wife: He published over 300 scholarly articles, with one notably holding a record for the greatest age gap between co-authors.
Guy's wife Louise was a great supporter of his work, and without naming the source Wikipedia tells us they, Richard Kenneth Guy and Nancy Louise Thirian, married in December 1940. The university website tells us she gifted him the "Louise and Richard K. Guy Lecture series" as a contribution to the University for his 90th birthday. Guy never really retired from his work at the University, they only stopped paying him after his official retirement in 1982, he said. The website clarifies: Even as his age entered triple digits, Richard often spent five days a week at his office in the Department of Mathematics and Statistics.
There is a long list of books and articles written by Guy on the website, certainly only a part of what he published. But who was this man? How did he get there?
We will use the Wikipedia entry as a (tertiary) source, so readers should check with the secondary sources listed there, to which I have no access.
Guy was born on 30 September 1916 in England as the child of two teachers, which as well as reading Leonard Dickson's "History of the Theory of Numbers" at the age of 17, gave rise to his love for mathematics. In 1935 he went to Gonville and Caius College, Cambridge, where he started composing chess studies, and also gained interest in games in general. After his graduation in 1938, only with a second-honors degree due to his obession with chess, he decided to become a teacher.
In Cambridge, he met his future wife, marrying in December 1940. Notably, he was 24 years old at that time, meaning that their love, which lasted for life, still benefitted both for three quarters of a century. The marriage gave birth to three children, notably on 1 April 1943 the computer scientist and mathematician Michael Guy, who also would go on to work closely with John Conway.
After some turbulent years abroad, Guy met Paul Erdös in Singapore in 1960, collaborating on four papers. Guy's interest in unsolved problems, one of which posed by Erdös he solved himself, led to his writing of two such books, including "Unsolved problems in number theory". Eventually Guy decided to stay abroad, In 1965 he permanently joined the staff at the University of Calgary, from which he officially retired in 1982, but in reality just worked as before, five days a week, without their payment.
Guy's contributions are too much to list here, and while we talked about his books and research papers before, Wikipedia lists the names of many of his co-authors, which include many famous mathematicians of the 20th century, such as Kenneth Falconer (whose digital sundial is a fascinating idea) and Neil Sloane, who might be best known to younger readers as a Numberphile video contributor.
Richard and Louise Guy shared the love for environmentalism, hiking, mountaineering (including climbing), winter sports, and likely many other outdoor activities. The Wikipedia article states, with appropriate sources:
In 2014, he donated $100,000 to the Alpine Club of Canada for the training of amateur leaders. In turn, the Alpine Club has honoured them by building the Louise and Richard Guy Hut near the base of Mont des Poilus.
Among my many compositions, two were anticipated by a guy with exactly that last name, not knowing who exactly that author was. In 2004 I stumbled upon a small idea, anticipated by a certain "R. Guy". I wondered who this composer was: A Frenchman? Someone who fought in the Spanish Civil War? The name sounded a bit like that. With his chess studies ending in 1954, it was certain that this man was a long-forgotten hero from the past. I had accidentally re-composed one of his studies, back then listed in the database as from 1949.
Richard Guy, British Chess Magazine 03/1945. White to move and win
Re-composition 2004. Black to move, White wins (unpublished due to anticipation)
1.Ne1+ Kc3 2.h6 a2 3.h7 a1Q 4.h8Q+ Kb3, and now taking on a1 leads to stalemate, so... 5.Qg8+ Kc3 6.Qg7+ Kb3 7.Qf7+ Kc3 8.Qf6+ Kb3 9.Qe6+ Kc3. Here our solutions differed. Guy gave 10.Qe5+ Kb3 11.Qd5+ Kc3 12.Qd3+ Kb2 13.Qc2+ Ka3 14.Qa4+ Kb2 15.Nd3+ Kb1 16.Qb3 or Qd1+ wins, but armed with modern technology my solution was 10.Qe3+ Kb2 11.Qd2+ Kb3 12.Qb4+ Ka2 13.Qc4+ Kb1 14.Qc2 mate.
My next accidential re-composition of a Guy study was in 2012.
Richard Guy, "Richard Guy's Endgame Studies" 1996. White to move and draw
Re-composition 2012. White to move and draw (unpublished)
Guy composed his study in November 1938, and this time we again only mostly agreed on the solutions: 1.c7 h1Q 2.c8Q Qh2+ 3.Ka8 Qg2+ 4.Kb8 Qg3+ 5.Ka8 Qf3+ 6.Kb8 Qf4+ 7.Ka8 Qe4+ 8.Kb8, and unfortunately e5 is inaccessible to Black and c5 is accessible to White. So there is only a draw with 8.-Qe7 9.Qc5+ Q:c5 10.d:c5+ K:c5 11.Ka7/Kb7 Kb5 12.b3 Kc5 13.Ka6 draws. Mirrored, I had preferred 11.-b3 12.Ka6 Kb4 13.Kb6 Kc4 14.Ka5 draws
At least this time I knew who Guy was: The inventor of the GBR code.
I don't remember when I learned not only that Guy was still around but that he also was the greatest amateur mathematician of the 20th century. However, when I did I was astonished. Suddenly that chess composer from an old era was someone who still could be admired today.
In some way I have to regret never seeing his great work during his lifetime, never having the chance to tell him about my admiration, of which only a tiny part will be conveyed in the replayable studies below, and maybe a greater part if you watch the Hackenbush video linked further above...
I still owe you the solution to the riddle above:
16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17 (Bernardo Recaman Santos, 2000) looks very random at first, but if you have a look at neighboring numbers, you see that their sums add up to squares. 16+9 = 25 = 5²; 9 + 7 = 16 = 4²; 7 + 2 = 9 = 3², and all other sums are one of those three.
It is left as an exercise for readers to read the article by Berlekamp and Guy in Crux Mathematicorum, October 2020, linked also above.
