Summer knight city

Study of the Month: June 2021

Casually reading through an older issue of EG, I found a nice study from the Kalandadze-MT 2019. It inspired me to write a bit more about knight promotions. Later on, I found that a few other knight endgames and other setups can also serve as illustrations of the knight’s possibilities. Here’s a “Pro” tour: Promotions, Professions and Proportions.

Promotions

Not always can a fancy or interesting story accompany endgame studies — this month, more practical matters will be talked about. When I recently read an issue of EG from 2020, I noticed the following study.

Magical Chess Endgames Vol. 1 & 2 + The magic of chess tactics

In over 4 hours in front of the camera, Karsten Müller presents to you sensations from the world of endgames - partly reaching far beyond standard techniques and rules of thumb - and rounds off with some cases of with own examples.

The study is very much self-explanatory, possibly with the lone pitfall of 1.Rh5+? Kd6 2.R:c5 f:e2 3.c7 e1Q 4.c8Q Qf2+ (or 4.Rc6+ K:c6 5.c8Q+ and Black wins the endgame with any move, but in practical play would have to still face issues) as a variation one could fall for.

1.e7 Kd6 2.e8N+ R:e8+ 3.K:e8 Re5+ 4.Kd8 f:e2 5.c7 Re8+ 6.K:e8 e1Q+ 7.Kd8 Qe6 8.c8N+ draws.

The tourney’s theme was what I call “Georgian material” — i.e. only kings, rooks and pawns in the initial diagram. The study here shows two promotions to a knight, while Black has active counterplay. The material invited to tactical fireworks like the one shown above, but also to endgame studies that indeed are endgame studies.

Mikhail Zinar [pictured], about whom we reminisced earlier this year, showed five promotions to queen on different squares to eventually reach a stalemate that was set up early, which expanded on his earlier tasks without being one in itself. However, due to the back rank mates being easily obtained in rook endgames, knight promotions are easy to create as well — always using the same pattern of preventing checkmate. When new aspects or multiple promotions come into play, it gets interesting.

That not every promotion to a knight similarly to the study above can save the game for the promoting side is self-evident, especially in the corner. The study from Moravec that I presented last month is a good example. As you had enough time to solve it, the solution is given on the replayable board below.

It is of note — Tim Krabbé, in fact, has a selection of such occurrences in practical play — that underpromotions, when they are necessary, to bishop or rook can only be motivated (in orthodox play, i.e. games, studies or directmates) by stalemate. The defending side may underpromote so that the new piece is unable to move, or the attacking side may underpromote so that the opponent can still move. One of the most basic examples is the position wKc6, wPc7, bKa7 where 1.c8R checkmates in two moves. The problem is originally by Edward John Catlow (The Saturday Magazine 741, 20 January 1844). It was famously reprinted by Tomlinson in his book Amusements in Chess where he omitted the author (thanks to Andrew Buchanan and the Schwalbe Problem Database PDB for the information!).

Knight promotions can be motivated by stalemate in the same vein, but usually the difference between the movements of queen and knight, i.e. the immediate necessity to attack or protect one of the squares a knight could reach but a queen couldn’t, is the motivation for such promotions. Thus, the term ‘underpromotion’ here applies only by the usual value of the pieces, not their movement patterns.

We had already talked about pawn endgames with task promotions to knight, i.e. as many as possible. Recently, I presented Zinar’s study in which he, after other composers had done it before, showed five such promotions. Of greater practical value are settings that might occur in actual games. Obviously, promoting to a knight works at any point in a game, be it in the opening, as in Xu Jun - Ivanchuk, Luzern 1993; in the middlegame, as Suat Atalik [pictured] once demonstrated in a famous game against Tony Miles in Iraklio the same year; or obviously in the endgame. Only very rarely does a knight promotion leads to a beautiful pattern like in the following ending of the correspondence game Maiorov - Rakhmatullin, 1996 (taken from the book series Wij presenteren by Hans Böhm & Yochanan Afek, in the book about De Pion).

Black is ready to deliver checkmate, but White can draw with 1.e8N+ Kg8 2.Nf6+ Kg7, etc. Instead, he won with the fork 1.Bf6+! K:f6 2.e8N mate.

The book Het Paard of the Böhm/Afek series has a page about Phoenix promotions. A knight is captured first, and then is “reborn” by a promotion. This is based on an old Greek mythological bird called the Phoenix, which is said to be reborn from its own ashes again and again. The card game ‘Magic: The Gathering’ had a very annoying card years ago with a similar idea, and while many phoenixes exist in that game, this one stood out. It turned into an egg upon death, and that egg hatched back into the creature if it survived.

Possibly, this is a better analogy to the chess phoenix. Or possibly a less romantic view is in order, whereupon a knight dies, and another one is sired from a serf. In German, the pawn is a ‘Bauer’, a farmer. In medieval times, a farmer could become a knight — most famously, Johanna of Orleans liberated an entire country, stemming from a farmer’s family and having the courage to become a legend. Her grim fate afterwards does not apply to all chess knights.

Two endgame studies from that Feniksthema page of the book are replayable in the widget at the end of the article: Kasparyan (1978) and Afek (2011).

Professions

Knight promotions have many more aspects than the ones shown above, but I’d like to consider their role in the battle for promotion as well. The number of endgame studies where a well-placed fork of king and knight by a knight ends the play is rather large. Not always is a fork the end all be all. Additional ideas need to be executed sometimes, such as when, already a century ago, Rinck demonstrated that the fork might win a tempo for a pawn to shut off the opposing knight.

Chess Endgames 12 - Rook vs Knight

What is the best way to use your pieces to their full potential in the endgame? GM Karsten Mueller demonstrates "knight geometry", and teaches you how to employ the "knight check shadow" in your own games!

1.Ne7! Nd7 2.Nc6+ Ka6 3.Nb8+ N:b8 4.g7 wins, or 2.-Kb6 3.N:e5 Nf6 4.Nd7+! N:d7 5.e5! wins

Additional finesses can occur in such endgames when for example checkmate is invoked. With this information, the following endgame study is left as an exercise for readers to solve. The solution is presented at the end of the article.

It seems that the draw after 1.f4 Ng2 2.f5 Ne3 3.f6 Ng4+ is unavoidable. Is it?

In an earlier article, I had shown another profession of knights: delivering the much-feared smothered mate. Not a smothered mate but the same kind of check to win the queen occurred in the following game where Black gave two pieces to deliver a check on the diagonal a7-g1.

Black was certain that the game is over after his combination 22.-Bb3 23.R:b3 Qa7+. 24.Kh1 Nf2+ 25.Kg2 N:d1 26.R:b4 Qf2+ 27.Kh3 Q:f3 seems forced, and in view of 28.R:d1? Qh5+ 29.Kg2 Q:e2+ and 30.-Q:d1 White can resign. Black was right, the game was over, and resignation followed promptly... The one resigning was him, though, after 24.Nb6!!, which after 24.-Q:b6+allows White to move either his queen — exchanging the powerful pieces — or even the other knight to d4.

The basic idea was correct, of course. In the diagrammed position Black needs to take on e2, and White can’t take with the bishop due to the deadly check on a7. So 22.-B:e2 23.Q:e2 R:a4 24.R:a4 Q:a4 follows, and the fork on d4 prevents White from taking the knight. After 25.Qb2+ Nf6 Black remains a pawn down and will have a difficult defensive task, but he was able to play on. Adding insult to injury, after Dyner’s 22.-Bb3 Oren had other ways to win: 23.Qc1 Qa7+ 24.Nc5 is one example, and here even 24.Kh1 wins: 24.-Nf2+ 25.Kg2, and the threat of the fork on c3 prevents Black from winning back his minor piece.

Proportions

We had a look at a knight tour quickly at the end of another article a while ago. Het Paard gives the following one (among others), which is also a magic square, summing 260. The same diagram is found in a German language book about chess and mathematics (see below).

Power Play 15 - Practical Pawn Endgames

Based on his own playing experience, Grandmaster Daniel King reveals what is essential knowledge, saving you time in your studies. In the first section of the DVD he takes you through typical motifs and themes. In the second section he tests your knowledge with typical scenarios from actual games.
Video: 4 hours.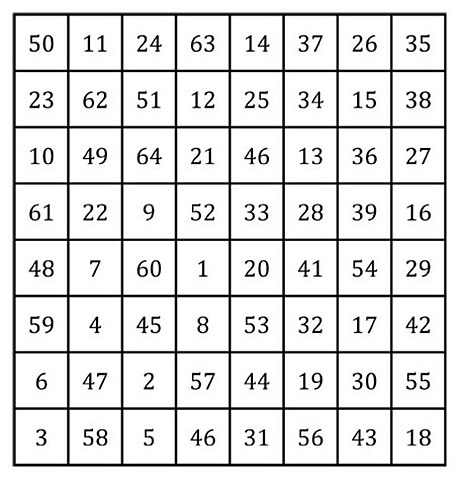

Eero Bonsdorff, Karl Fabel and Olavi Riihimaa presented the book Schach und Zahl in 1966. In it, they noticed that no magical knight tour diagram was found yet in which the long diagonals also sum up to 260. The diagram is symmetric in the sense that switching the first 32 moves by 180 degrees gives the other 32 moves. It also is a ‘closed’ tour, as the first and 64th squares are one knight move away, so the tour could be repeated ad nauseam. The book notes that on a 7x7 board, a closed knight tour obviously is impossible.

There is no closed knight tour on a 4x8 board either. An example for an open knight tour on a 4x8 board is presented below. If you look only at the lower half, it is also ‘symmetrical’ — i.e. it repeats itself on the top half of the board to a full knight tour (taken from Het Paard).

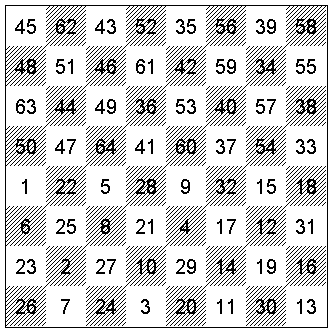
While not related to endgame studies, readers might be interested in a bit of fun mathematics. The following problems and solutions are taken from the book (explanations slightly altered).

Eero Bonsdorff, Helsinging Sanomat, 20 December 1961: How many different shortest games exist that can end in a draw?

As the draw can be claimed by threefold repetition, it means that the knights must move to and fro twice, allowing a draw after the fourth move. White has four different possibilities each for two moves, and Black as well. This gives 4² (that is 16) multiplied by 4² (again, 16) for a total of 256 different possibilities to reach the starting position again after the second and the fourth moves.

S. Urpo, Suomen Tehtäväniekat 1960/1961, 1st honorable mention: Black tries to play symmetrical to White. How big is the number of shortest games in which White can prevent this?

A check is possible at the third move of White after, for example, 1.Nc3 Nc6 2.Nd5 Nd4 3.Nf6+, or 1.e4 e5 2.f4 f5 3.Qh5+. Knight, bishop and queen are the three pieces that can give a check, and owing to ideas like 1.e3 e6 2.Bb5 Bb4 3.B:d7+, all three pieces have multiple variations. The total number of such variations is 48, with the following beginning moves and number of variations: 1.Na3: 3, 1.Nc3: 6, 1.c3: 4, 1.c4: 6, 1.d3: 1, 1.d4: 4, 1.e3: 9, 1.e4: 12, 1.f4: 2, 1.g3: 1.

While there is no complete list of all variations in the book, it is likely that readers will easily find them.

We will end our article with a problem by Eeno Bonsdorff and I. Mäkihovi, Ilta-Sanomat, 31 December 1960 (technically a fairy chess problem): How big is the number of shortest games ending in checkmate in which both players always make the geometrically longest move?

In fairy chess, this condition would be known as a ‘double maximummer’. However, readers need no experience with that condition, only an understanding that a move along a diagonal square has the moving length of the square root of 2, a knight move the square root of 5. The checkmate that is sought is by the queen on f2, assisted by a knight on g4. White must block the queen’s way back by moving one of his knights to g5. One variation is 1.Na3 Nf6 2.Nc4 Ng4 3.Nd6+ e:d6 4.Nf3 Qh4 5.Ng5 Q:f2 mate.

Readers will note that Black can move his knight to e4 and the longest move by the h4-queen still is Q:f2 mate. However, this is practically impossible, as the knight on e4 would be forced to take on d6 after the check: 1.Na3 Nf6 2.Nb5 Ne4? 3.Nd6+ N:d6 is geometrically longer than e:d6.

The b1-knight has four ways to get to d6, while both knights on the kingside have two ways each to reach g5 and g4.

So the solution is 4*2*2 or 16 variations. 

The knight is a versatile piece - it can, after all, reach any square of a standard chessboard from any other square in at most six moves — not only for endgame studies or practical play, but also for mathematical and recreational chess problems. While our monthly article diverged from our usual focus on endgame studies, six of them, talked about in the article, can still be replayed below.

Click or tap an entry in the list to switch positions

You probably know that you can move pieces on our replay boards to analyse and even start an engine to help you. You can maximize the replayer, auto-play, flip the board and even change the piece style in the bar below the board.

At the bottom of the notation window on the right there are buttons for editing (delete, promote, cut lines, unannotate, undo, redo) save, play out the position against Fritz and even embed the ChessBase game viewer on your website or blog. Hovering the mouse over any button will show you its function.

Answers to questions regarding tournament’s judges

Our reader Frits Fritschy followed the call to ask questions about judging and wanted to know in the comments of last month’s article:

Master Class Vol.10: Mikhail Botvinnik

Our experts show, using the games of Botvinnik, how to employ specific openings successfully, which model strategies are present in specific structures, how to find tactical solutions and rules for how to bring endings to a successful conclusion

I wonder how much something like ‘clarity of play/cohesion’ is part of the things an endgame study judge is looking at, and how important it is. I’ve seen prize-winning studies with an interesting idea in it, but with an introduction that is hardly related to that idea. [...] Also, isn’t ranking studies in a tournament sometimes comparing apples and oranges? For instance, the study by Becker and Akobia is highly theoretical, which in my opinion adds something to the knowledge of the game. In contrast, the study by Eschbach is mainly a tactical fight: it’s not about knowledge, but about ideas. 

I had answered briefly in the comments section, and unfortunately can’t add much more. I might have slightly wrongly used the term ‘clarity of play’. It means to me that the play is understandable and clear to humans. ‘Cohesion’ is what the question seems to be about, i.e. that the introductory play to a study is incoherent with its later appearing main idea. Here I must add that a good introduction can add to the appeal of an endgame study, while a bad introduction subtracts. If an introduction is incoherent, a judge might choose to ignore it and award the study for the merits of the main point. However, he should clearly state so in the award.

A composer with a similar name, Jindřich Fritz, made an art out of introductions, using forced but deeply flowing play to reach an economic final position. Possibly, the Czech master wanted to escape the confines of classical ideas when he composed the study that we added on the replayable board above.

Ranking studies in a tournament is indeed often a difficult task, as their styles might be completely different. I am far from an expert in that field, but personally I would rank them intuitively while also applying a basic analysis first to determine if they are eligible to receive an award. This analysis consists of two parts: checking for anticipations and checking for correctness. The former is possible by searching for patterns and positions in databases. The latter requires analysing the study with a good hardware and software. Ranking a theoretical study and a tactical study in the same tourney might justify an ex aequo solution where both studies are awarded (hypothetically if they are good enough) a shared 1st/2nd prize, or any other place in the ranking that feels appropriate.

In the end, judging comes down to the personal preference, experience, and personality of the judge. I tend to give rather few awards, it seems, but also rate endgame studies higher on a point scale than others. This paradox remains unexplained to me, unless we accept the explanation that at the one time, when I had to use a point scale, the studies already were of a higher-than-usual quality.

Endgame Turbo 5 USB flash drive

Perfect endgame analysis and a huge increase in engine performance: Get it with the new Endgame Turbo 5! This brings the full 6-piece Syzygy endgame tablebases on a pendrive. Just plug it in a USB socket and you are set!

World Federation for Chess Composition (www.wfcc.ch)

Links

• May 2021: A judge’s rant to the awards galaxy
• All study of the month columns