Study of square utilization and occupancy

By Devin Camenares

Introduction

As a chess player, I always seek ways to improve my game. As a scientist, I look for hidden connections within large sets of biological data. Finally, as a professor, I’m interested in finding new ways to explain and demonstrate the scientific method to my students. I’ve often wondered if I could combine these three endeavors: is it possible to leverage large databases of chess ‘data’ to apply a scientific approach to the game? While I can’t claim to have an answer to this open-ended question, I have created a suite of simple, easy to use, and freely accessible tools that might be helpful in chess research.

These tools can be used to analyze the number of moves a particular piece makes to any given square, or the number of positions where you find a particular piece on a given square. In other words, you can determine the square utilization and occupancy for any and all pieces and squares, across all moves and positions in all games in a PGN database. In addition, there is a simple tool to reformat PGN or create a chessboard heatmap. I was motivated to develop these tools for several reasons. First, the coding was good practice for the development of other programs needed for my life science research (i.e. a nice way to teach myself JavaScript). I was also inspired by the chess visualization study by Seth Kadish, featured at ChessBase last year, among other chess studies.

In fact, the tools I created can recreate some of the work done by Kadish; namely, looking at the aggregate square utilization for the white pieces, as played by Fischer or Carlsen.

Fischer versus Carlsen as White

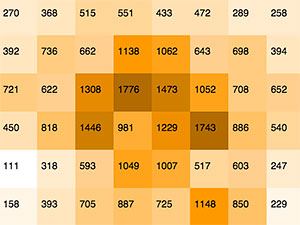
In the figures above, a chessboard heatmap is shown, with the inset numbers representing the number of times a White piece landed on that square across all the games in the database used. The darker the square color, the higher the value. It’s not surprising that there is a lot of ‘traffic’ in the center of the board, and that there only minor differences between these two world champions.

In addition to looking at square utilization, I also created a tool for examining square occupancy. Applying this to the same dataset reveals a different pattern:

Comparing both the square utilization and occupancy, we might conclude that both players move their central pawns, develop pieces through the center, and generally keep their Kingside structure intact (in particular, there is usually something placed on g2, whether it be a pawn or bishop). While looking at the square utilization data alone might lead you to think Fischer preferred 1.d4, both datasets together make the situation clear: he preferred to first plant a pawn on the e4 square and then open lines and mobilize his pieces through the d4 square (i.e. any Open Sicilian, which starts with 1.e4 but more heavily utilizes the d4 square, with moves such as 3.d4 cxd4 4.Nxd4).

Difference Makers in Fischer’s Games

We can also take a closer look at the above data, and examine the square utilization and occupancy for individual pieces. For this type of analysis, I have found it more interesting to consider Fischer’s wins and losses with white as separate databases. Shown as an example is the utilization and occupancy (or ‘traffic’ and ‘parking’) of the white knights.

You can see that there are some similarities to this pattern, but also slight differences. After normalizing the number of moves in each set, we can then subtract the values from the losses from those found in the wins. In essence, we are looking for piece placements or square utilizations that are found more often in wins or losses. This ‘differential’ data set can also be plotted as a heatmap; here, positive numbers or orange represent squares that occur more often in White wins, while negative numbers or blue represent squares that occur more often in losses. (The scale is such that a value of 10 represents a square that is featured one percentage point more in wins versus losses).

Perhaps unsurprising, this data suggests that an advanced knight, particularly one travelling to the f6 square, is more often found in Fischer wins as white. While the square utilization data highlights transient travel through f6, the occupancy analysis paints a different picture: a stable knight on f3, controlling central dark squares, also correlates with White victories. An interesting result is the positive differential for a b1 knight. One possible explanation is that this represents games in which Fischer scored a quick and violent win, a game so short that he did not need to complete his development. This same analysis can be done with any pieces in this database, white or black.

Examining the white king in Fischer’s game might also be explained by common chess wisdom. An uncastled King stuck on e1 appears to be found more often in a loss, while a castled king correlates with a win. Advanced king moves on the kingside, most likely in the endgame, appear to contribute to success. I can’t help but wonder if this reflects in part Fischer’s choice of the Ruy Lopez Exchange variation.

Difference Makers in the Opening

Studying which squares makes a difference in a player’s games could be interesting, but perhaps not that useful unless you planned on facing Fischer or Carlsen in your next club tournament. More interesting and perhaps useful is to take the same approach with an opening database, comparing datasets from wins and losses in your favorite opening. As one final example, shown below is the differential data for the white queen in several thousand games with the SicilianSveshnikov played in the last fifteen years.

From this we might conclude that White should strive to use their queen in attacking the light squares on the black kingside. Conversely, if White is spending time using the queen to cover squares like d3 and d2, Black has probably already seized the initiative. While interesting, it’s important to note that the data only gives hints at correlation; the idea that it is important for the queen to penetrate these square thus remains a hypothesis to be further tested by examining the games themselves (but at least you have a target to examine!)

Ideally, I would continue and expand this analysis, and may occasionally post results at my blog, Science on the Squares (which also contains more detailed information on the process and the heatmaps). However, with the start of a new semester my profession responsibilities place a formidable demand on my time. I invite any readers to use these tools in their own chess research, and to share their results and insights with the chess community, here or elsewhere.

About the Author

Devin Camenares is an Assistant Professor in the Department of Biological Sciences at Kingsborough Community College, and resides in Yonkers, NY. He attended Rutgers University as an undergraduate, and later earned a Ph.D. in Molecular Biology from Stony Brook University. If he is not teaching, doing research, or spending time with his new wife Vicki, you will probably find him staring at a familiar set of 64 squares.