Rating Inflation - Its Causes and Possible Cures
By Jeff Sonas
A few weeks ago, I wrote a news article for ChessBase in which I summarized the discussions and conclusions of the recent K Factor meeting in Athens, Greece. In that article, I promised that I would have much more to say about some of the topics.
I did a lot of analysis in preparation for the Athens meeting – it was very enjoyable to delve back into chess statistics after taking a couple of years off from it – and I have many things I want to share. Ultimately I have three different areas I want to cover: rating inflation, the accuracy of the FIDE rating system, and finally the K Factor itself. As my first installment, I would like to discuss rating inflation, a relatively controversial topic.
First of all, what does the term "rating inflation" actually mean? Some people would say it means that a player with rating X today is not as objectively strong as a player with rating X was in the past. For example, thirty years ago a 2620 FIDE rating would have meant you were a world championship candidate, whereas today there are more than 30 Russian players with FIDE ratings above 2620. How do those 30+ Russian players of today compare, objectively speaking, to players like Lev Polugaevsky, Jan Timman, Bent Larsen, or Mikhail Tal from thirty years ago?
Of course this is difficult to assess objectively. We don't have a great means yet of measuring the objective quality of a player's moves. Attempts have been made to measure the strength of players by running their moves through a strong computer engine and seeing how well they match, but of course that can say more about how "computer-like" a player was, rather than objectively how strong their moves were. I do think that there is value in this type of analysis but I think it needs to be performed across larger groups of players. Probably it could give us a very useful calibration factor that would indicate how much players have improved over the years. I would be surprised if we don't have much more progress on this within the next five years. However, that is a topic for another time.

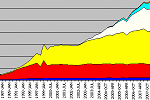
Inflation? Players rated 2700 or higher in 1979, 1994 and 2009
Another related use of the term "rating inflation" would be to indicate that a previously elite club, such as all players rated 2700+, or all players with the grandmaster title, has become much less exclusive. As an example, thirty years ago (in 1979) only the world champion Anatoly Karpov was rated 2700 or higher by FIDE. Fifteen years ago (1994) there were six players in the 2700+ club. And today, on the July 2009 FIDE list, there are thirty-three players rated 2700 or more! You see similar effects when counting up the number of grandmasters (the grandmaster title is partially based on reaching a certain minimum rating, so it is affected by inflation as well).
So clearly the 2700+ rating and the grandmaster title are less exclusive than they used to be. On the other hand I'm sure many people think that the ratings have faithfully kept up with the general improvement in chess skill, and so it would make sense that we have more grandmasters or more players rated 2700+. However I don't believe the data supports this explanation for why ratings have gone up.
I have my own way to describe inflation, which is to look at how the rating of the #X player on the rating list has increased over time. I don't like to use measures that are affected by the inclusion/exclusion of weaker players in the rating pool, so that would rule out a measure such as the average rating of all players. I like the idea of just counting down from the top-ranked player to a particular Nth world rank, and seeing how the rating of that world rank has changed over time. That approach takes us to this very important graph:

First of all, I find it to be very interesting that between 1975 and 1985 there was no significant inflation at all (by my definition at least). For instance, look at these three subsets of rating lists (including just the #5, #10, #20, #50, and #100 players) between 1975 and 1985 – there is really no difference among them:
|
Rank |
January 1976 list |
January 1980 list |
January 1984 list |
|
#5 |
2630 (B.Spassky) |
2635 (L.Polugaevsky) |
2630 (U.Andersson) |
|
#10 |
2620 (H.Mecking) |
2605 (F.Gheorghiu) |
2615 (V.Hort) |
|
#20 |
2575 (S.Gligoric) |
2590 (B.Gulko) |
2575 (G.Sax) |
|
#50 |
2530 (B.Malich) |
2535 (J.Pinter) |
2525 (M.Suba) |
|
#100 |
2490 (L.Ogaard) |
2500 (L.Vadasz) |
2490 (V.Inkiov) |
I should point out that there were barely 1,500 active players on the January 1975 list, and that number more than tripled in ten years, to more than 4,600 active players on the January 1985 list. Nevertheless there was no inflation (using my meaning of the term). So the argument that inflation is a natural result of the general advance of chess knowledge would not explain why there was no inflation across those ten years.
Another common explanation for inflation in the top 100 is that the pool of players is getting bigger, and thus it would make sense that the top 100 (which is really just the right edge of the bell curve) is shifting further and further to the right (and thus has a higher and higher rating). I do not agree with this explanation. I don't think we are adding in players anymore at the right edge; I think we are adding in players at the left edge, via inclusion of new provisional players or via the reduction of the rating floor. I also think that if we were just grabbing a larger sample of players of all strengths, we would see a progressively smaller rating gap between #100 and #500, or between #100 and #1,000, etc. However this is not at all what the data shows. In fact those gaps are incredibly constant across time. Look at the flat white/yellow lines in the following graph:

So I do not believe we can explain away this inflation through the simple fact of the rating pool increasing. I would very much welcome input from other mathematical or statistical experts as to whether we would expect to see the gap closing if we were adding more players across the whole distribution. I'm pretty sure I am right, though…
Anyway, back to the actual data. Starting around 1984 or 1985, we see the ratings of each spot on the rating list steadily increasing by about 7-8 points per year, for about a dozen years. For example, if you look at that same table again for 1987, 1991, and 1995, it is very easy to tell which list is which! This is consistent with the idea of overall rating inflation of 30 points every four years:
|
Rank |
January 1987 list |
January 1991 list |
January 1995 list |
|
#5 |
2625 (V.Korchnoi) |
2650 (E.Bareev) |
2715 (V.Salov) |
|
#10 |
2605 (B.Spassky) |
2640 (U.Andersson) |
2675 (E.Bareev) |
|
#20 |
2585 (A.Beliavsky) |
2620 (R.Huebner) |
2645 (I.Sokolov) |
|
#50 |
2550 (J.Speelman) |
2575 (M.Chandler) |
2605 (G.Kaidanov) |
|
#100 |
2515 (S.Makarichev) |
2545 (K.Lerner) |
2575 (I.Gurevich) |
Then starting around 1997, it levels off some, to the point where we are now seeing an inflationary rate of about 4 points a year. This is not just true within the top 100, but is true well down in the rating list. For instance look at this graph:

Again I find it fascinating that the inflation is so relentless. Look at the white and yellow lines, indicating the ratings of the players ranked #500 and #1,000, respectively, on each FIDE rating list. You can see the inflation start in 1985, and then level off a bit in 1997, but it's still going up. Since 1985 we are looking at a total shift of about 130 points upward, a massive increase.
Such a steady inflation almost certainly comes from a systematic effect, rather than an isolated incident such as the 100 point bonus that was awarded to all women other than Susan Polgar in 1986. I am unsure as to where the inflation comes from, or how to halt it. I should also point out, in a quick preview of part III of this series, that inflation was a key reason why I ultimately found myself opposing the doubling of the K-factor during the Athens meeting. It appears that doubling the K-factor would add an additional 7 points per year of inflation, above and beyond the 4 points per year that we are already seeing. We would be awash with grandmasters and 2700+ players, in hardly any time at all.
Finally, I would like to explain my current theory as to why there is inflation. I first heard this explanation in Athens from Nick Faulks, and I see no flaw in it. Here is how the argument goes
There was originally a very high rating floor. Over time it has gone lower and lower, but for a while it was 2200. This meant if your rating was calculated to be 2200+, then you would show up on the FIDE list, but if your rating was calculated to be below 2200, then you would completely disappear from it. That's why for a long time there were no men rated below 2200 (the women had a lower rating floor initially, I think). You can clearly see the impact of the rating floor of 2200 and then (later) 2000 in this stacked area graph which indicates the overall distribution of players across time:

Now let's think about how it was back when the rating floor was 2200. Consider a hypothetical group of active players, all of whom have a performance rating of 2000 across all their games. Some of those players will certainly outperform their true 2000-strength for a short time, and others will underperform. Only those players from our group that outperform their true strength will make it onto the rating list, whereas the players who underperform will not be anywhere on the list. This means the players who show up on the rating list just above the rating floor, are (as a group) significantly overrated, just waiting to donate rating points to the rest of the pool. Even worse, while these overrated players keep temporary possession of their 2200+ ratings, other players may also receive inflated initial ratings as well, based partially on games against the overrated players. Over time, the overrated players will do worse than their ratings suggest, and their excess rating points will ultimately be distributed throughout the entire rating pool.
If this argument were true, you would expect to see that provisional players (i.e. those players who have not yet played 30 games) on average are actually losing rating points during their time as provisional players. And in fact this is what the data does appear to show. Although you would think that newer players are still improving and would in fact gain points on average, it seems clear that provisional players are actually being overrated. This needs more investigation, and I still don't fully understand why the inflation rate has changed so much over time.
One possible approach would be to modify the formula governing how players receive their initial ratings. Currently it is fairly reasonable in that if you score 50%, then your initial rating will be exactly that of the average opponent rating you faced. But perhaps it should be somewhat lower than it currently is, no matter whether you scored 50%, or higher, or lower. This point is actually independent of the rating floor; in theory by looking at historical data, we should be able to tell how to come up with a formula for initial ratings that does not overrate new players on average. I am still thinking about this one.
In closing, let me say that I am hoping, by raising inflation as an issue, to get a healthy discussion going, and ultimately figure out how best to correct it. Of course I also have built a rating-calculation model that would let me test various schemes and see their effect upon inflation over time, but again that is something I will talk more about in Part III. This is probably enough for now! Please feel free to send in your thoughts on rating inflation; I'm sure there are many strong opinions on the topic!
ChessBase Articles on the K-factor in the FIDE rating system
|

|
Ratings Summit in Athens
22.06.2009 – On June 11-12, FIDE held a special meeting in Athens, Greece to discuss the implications of changes to the FIDE rating system, especially the increase of the K-factor. Ratings experts from around the world (including John Nunn and GM Bartlomiej Macieja) were brought together to recommend a course of action to the Presidential Board. Jeff Sonas reports on the meeting. |
|

|
Rating and K-factor: wrapping up the debate
11.05.2009 – The discussions regarding the K-factor – the rate at which ratings go up or down when they are calculated – reaches its climax with a wrap-up article by Dr John Nunn, grandmaster and mathematician, who evaluates the arguments that have been presented by the different parties. After this it is up to FIDE, which has already initiated positive steps settle the matter. Final installment. |
|

|
Thompson: Leave the K-factor alone!
07.05.2009 – The debate on whether to increase the rate of change of the Elo list continues. Today we received an interesting letter from Ken Thompson, the father of Unix and C, and a pioneer of computer chess. Ken believes that the current rating system isn't broken and that the status quo is better than change. If anything the ratings should be published more often – every day if possible. Food for thought. |
|

|
Rating debate (6): Here comes the proof!
04.05.2009 – "I couldn't believe my eyes when I read GM John Nunn's opinion," writes GM Bartlomiej Macieja (pronunciation supplied), the original initiator of this debate. He presents proof for the fact, challenged by Nunn, that the K-factor and the frequency of rating lists are related to one another. Other readers have also weighed in, a wrap-up reply by John Nunn will appear soon. Long, interesting read. |
|
|
Rating debate: is 24 the ideal K-factor?
03.05.2009 – FIDE decided to speed up the change in their ratings calculations, then turned more cautious about it. Polish GM Bartlomiej Macieja criticised them for balking, and Jeff Sonas provided compelling statistical reasons for changing the K-factor to 24. Finally John Nunn warned of the disadvantages of changed a well-functioning system. Here are some more interesting expert arguments. |
|

|
Nunn on the K-factor: show me the proof!
30.04.2009 – With the debate raging over FIDE's decision to change or not to change the K-factor used in calculating players' ratings, we are glad to receive an important message from our voice-of-reason grandmaster. Dr John Nunn says "there seems no real evidence that K=20 will result in a more accurate rating system, while there are a number of risks and disadvantages." His explanation and reader feedback. |
|

|
Macieja: the FIDE General Assembly must decide
30.04.2009 – "Using the FIDE Laws of Chess terminology, the move has been made, and no takeback is any longer possible." Polish GM Bartlomiej Macieja is insisting that the decision to increase the K-factor in rating calculations is not just necessary and good in the current tournament situation, it is in fact irrevocable and can only be legally changed by the body that passed it. Open letter. |
|

|
FIDE: We support the increase of the K-factor
29.04.2009 – Yesterday we published a letter by GM Bartlomiej Macieja asking the World Chess Federation not to delay the decision to increase the K-factor in their ratings calculation. Today we received a reply to Maceija's passionate appeal from FIDE, outlining the reasons for the actions. In addition interesting letters from our readers, including one from statistician Jeff Sonas. Opinions and explanations.
|
|

|
Macieja: The increase of the K-factor is essential
28.04.2009 – Yesterday we reported that FIDE had decided not simply to change the K-Factor in its rating calculation, but to publish two parallel lists for a year and then review the results. Today we received a passionate appeal by GM Bartlomiej Macieja not to delay the decision but increase the K-factor immediately. In fact he advocated recalculating the lists of the last two or even five years. Let the debate begin. |
|

|
FIDE: Anand-Topalov bidding, K-Factor
27.04.2009 – The World Chess Federation has opened the bidding for the next World Championship match between Viswanathan Anand and Veselin Topalov, scheduled for April 2010. At the same time FIDE has reacted to concerns of players and decided not to simply change the K-Factor in its rating calculation, but to in fact publish two parallel lists for a year and then review the results. Press releases. |