Putting his money where his stats are

Part V: Are you a betting man (or machine)?

Part I • Part II • Part III • Part IV

One of the neat things about chess ratings is that they give us a way to calculate the estimated odds of winning a chess event. If you were a frequent visitor to the KasparovChess website during its three years of existence, you probably read several of my tournament articles where I would calculate everyone's chance to win, using statistical models and random simulations. I think I exhausted every possible variation on the phrase "Garry Kasparov is the statistical favorite to win...", because the highest-rated player in the world was inevitably the favorite, whenever he played.

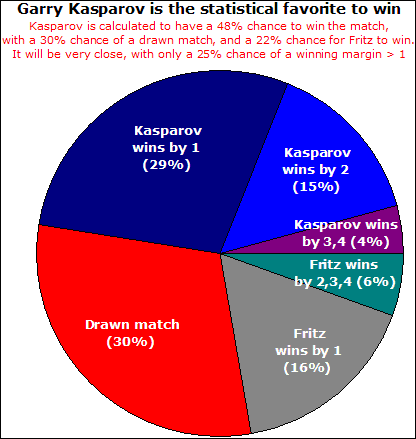
Based upon my latest statistical model, I have calculated that Kasparov is indeed the statistical favorite again, with a 48% chance to win his four-game match against X3D Fritz. There is a 30% chance for the match to end in a 2-2 draw, and a 22% chance for Fritz to win the match.

Kasparov is the highest-rated human player on the planet, with a FIDE rating of 2830. Computer ratings are much trickier to figure out, and there is no official list which relates to games against humans. I have been working on this computer rating problem for an entire year, and I am still very unclear on the best way to solve it. David Levy and the ICGA (International Computer Games Association) are sponsoring an effort to gather historical data about computer chess games, in an attempt to calculate historical computer ratings, and that effort is the source of most of my raw data. My best guess at this point is that Fritz's strength is about 2760, relative to a top human player. Of course, these calculations would all be very different if that guess turned out to be quite wrong.

Obviously, there are some very subjective factors which come into play when trying to make a statistical prediction for this match. How much of a factor will the virtual reality goggles be? And can Garry Kasparov overcome his natural aggressive playing style, which seems particularly unsuited for play against a strong computer, and instead play with the necessary amount of mechanical precision? If you read Part IV, you will remember that historically, Kasparov has performed considerably worse against computers than expected, which is not a surprise given his inclination to sacrifice material and win brilliantly. Ultimately, this is a subjective factor, and so I have decided upon a subjective penalty of 45 rating points for Kasparov, under these particular match conditions.

Kasparov definitely gains a relative advantage through the shortness of the match. As we saw in Part III, as a match drags on, the fatigue factor plays an increasingly important role for the human player facing an untiring machine. Even in a four-game match, fatigue will be an issue. I estimate that Kasparov will play 40 points worse in Games Three and Four than he will in Games One and Two. If there were a Game Five and Six, it would have been 130 points worse, rather than 40.

Because of the fatigue factor, it will be important for Kasparov to capitalize upon his opportunities in the first half of the match. If the match is tied halfway through, Kasparov's chances to win the match drop from 48% down to 33%, whereas Fritz's chances to win the match rise a little bit (up to 23%). At that point a draw would become the most likely outcome of the match. Of course, if someone actually does take the lead by the halfway point, they will become the overwhelming favorite to win the match, with about a 70%-80% chance to hold onto their lead until the end.

In chess it is very important to keep track of who has the white pieces, because there is a definite advantage to the player who keeps the initiative in the opening. It is tempting to say that everything will hinge upon who can manage to win once with the white pieces. In that scenario, the two big questions are "Will Kasparov manage to win once with White and draw the rest?" and "Will Fritz manage to win once with White and draw the rest?" However, I don't think it's quite that simple.

Admittedly, in Kasparov's twelve games against Deep Blue, the advantage of the White pieces was very great, with White winning six games and Black merely one game. However, the story changes in recent years, when you look at the top grandmasters against the top computers. During Vladimir Kramnik's match a year ago against Fritz, White won twice and Black won twice. In Kasparov's match earlier this year against Junior, White won once and Black won once. These are not isolated incidents; it seems that the advantage of the White pieces is much smaller at the very highest level, when computers are involved. When top-20 humans play against each other, it's worth about 50 rating points to be White. When they play against a computer, it's only worth half as much to be White.

Interestingly enough, you can see the same trend for Kasparov himself, when he plays against human opponents rated 2700+. In the decade leading up to the Deep Blue matches, Kasparov's games showed the standard pattern of a 50-point rating advantage for White. Over the past five or six years, however, Kasparov has stopped defeating his strongest opponents so frequently with the white pieces. On the other hand, he also is losing less often to them when he has Black. This implies that the initiative given to White is not quite as important in Kasparov's games any more, and so the advantage of White is only worth about 35 points when Kasparov plays a very strong opponent. Because of all of this, it looks like a 50-50 chance that we will actually see somebody win a game with the black pieces.

It is reasonably likely that we will see some decisive games. My calculations show a 52% chance of at least two decisive games, and only a 13% chance of four straight draws. Fritz has a 47% chance to gain at least one win, whereas Kasparov has a 69% chance of winning at least one game. However, the ESPN2 viewers will be disappointed to hear that there is a 97% chance that at least one of the games will end in a draw…

Feel free to contact me regarding these articles at: jeff@chessmetrics.com