Nunn problems: solutions and compositions

Last week, in an article entitled John Nunn these days, we gave you three helpmate problems and one study to solve. They were shown to me by John on a Cornwall vacation. While it may be a little difficult — or rather unfamiliar — for many readers, helpmates are in my opinion a very beautiful art form. Do play through the solutions and try to appreciate the artistry contained in these problems.

Knight tours

During our trip to Cornwall, we went on daily 'Nunn Walks'. These are defined as outings lasting between two and five hours and always involve a minimum of six steep climbs, breath-taking scenery, castles, the Atlantic Ocean — and logical puzzles. Here are a couple he gave me on one walk:

Click or tap on all landscape pictures to enlarge | Photo: Frederic Friedel

“This is an easy one,” John said. I was slightly wary, because when John says easy he could mean almost anything. “Suppose there is an ant on every square of a 7x9 chessboard, and at some moment all the ants crawl to an orthogonally adjacent square, that is left, right, up or down — but not diagonally. Prove that after this there must be at least one empty square.” I got the answer in a few minutes and bravely asked for something more difficult.

“Suppose you have a chessboard m squares up and n squares across. If m and n are both odd prove that a closed knight’s tour is impossible.”

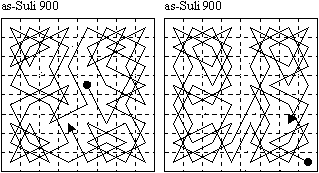A “knight's tour” on the chessboard is a sequence of moves by a knight such that each square of the board is visited exactly once. A “closed tour” is one in which the square at the end of a knight's tour is a knight move away from the first square. The master of Shatranj as-Suli published the two closed tours shown on the right.

I got this one very quickly as well, since it was rather similar to the ant puzzle, and said, “that was disappointingly easy.”

John smiled and went on: “That was just the first part. Now we will suppose that m or n is even.” — “What if both are even?” I asked, to which John commented, “when a mathematician says A or B, he means A or B or both.”

John explained the rest of the puzzle.

“You must tell me for which values of m and n a closed knight's tour is possible. I will give you the following information for free: there is no closed knight’s tour on the small boards 3x6 and 3x8, but apart from these two special cases there is a simple rule to determine, given m and n (at least one even), whether there is a closed knight’s tour on an m by n board. What is it?”

Of course one of the first things I did was to try to disprove the contention that the closed tour is impossible on a 3x8 board. I didn't use logic or any of that stuff, just good old brute force. In ChessBase you can draw arrows with the mouse by pressing the Alt key.

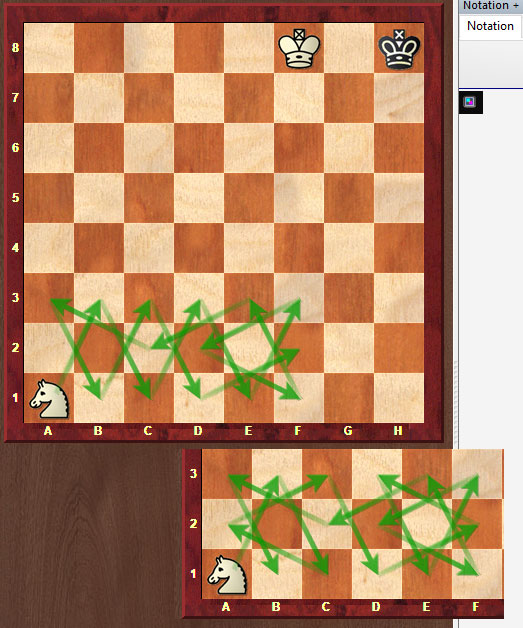
Half an hour of fairly unsystematic searching led me to conclude that John was probably right in this point: 3x6 and 3x8 do not allow a closed tour. But he wanted a rule to predict whether a closed knight's tour is possible for a given board, and I didn't even come close to solving this. So perhaps some mathematically inclined readers will help.

The Cornwall landscape is just breath-taking (click or tap to enlarge)

Youngsters getting surfing lessons on the beach

Soon they will be experts, surfing the ocean waves

A typical Nunn Walk in Cornwall. That's Merlin's Cave at the bottom right, to which we could not descend (high tide) and Tintagel Castle up on the cliff on the right, which we climbed up to, solving puzzles en route.

Another puzzle, back home at the cottage: “Have you considered that it is possible to place 32 rooks on the standard 8x8 chessboard so that whenever you choose five rooks, at least two must be attacking one another.” I replied fairly quickly: “Just fill the first four ranks. Then any selection of five rooks must include two on the same rank, and these will be attacking one another.” “Indeed”, said John, “but now suppose there are 33 rooks on the chessboard. Can you prove that however they are arranged, it is always possible to find five rooks such that no two are attacking each other. There is a simple proof.” Using M&Ms on a chessboard I had to concede defeat. Again: mathematicians please help!

At the cottage John was constantly honing his skills in solving chess problems (as described in my previous article), but he spent an equal amount of time doing math problems, taken from The University of Toronto Mathematics Competition. Here is a sample:

Consider the parabola of equation y=x^2. The normal is constructed at a variable point P and meets the parabola again in Q. Determine the location of P for which the arc length along the parabola between P and Q is minimized.

And why does he practice so hard? “Maths is fun and solving problems is fun, just like in chess — it's good to keep an active mind.”

John Nunn composing a chess problem, in the mid 1980s with an Apple ][

So now to the selection of John's own compositions of chess problems and studies. Please send in your solutions and comments to these and the mathematical problems using our “Feedback to the Editors”. We will pick a winning submission and John will send the reader a personally dedicated copy of his classic “Solving in Style”.

We start with a helpmate, hoping you have got used to them and appreciate their unique beauty. In this problem, for which John won third prize, we give you a substantial hint: White pins his own rook on the first move, unpins it using the knight on the second move and uses the unpinned rook to mate on the third move. In the second solution the roles of the two white pieces are exactly reversed. Easy to solve now? Remember it is Black to play and help White to construct a mate, of the black king, in three moves.

This recent problem won fifth prize. Two possible captures on a1 lead to the black rooks interfering with each other — in each case one rook blocks the other from making a vital capture.

If it were Black to move, then White could mate in 2, for example: 1...Kf4 2.Qe3+ Kg4 3.Qg3# or 1...d4 2.Qc5+ Ke6 (2...Kf4 3.Qf5#) 3. Bf5# But White has no move that simply maintains the situation.

For this study John won first prize. We leave you to solve it without any hints. If you are at a loss you can fire up a chess engine, although the solution is not completely trivial, for certain engines we know.

“The fact that Black is in zugzwang after White's first move is one of the most remarkable discoveries I made using an endgame tablebase,” John wrote in his book. “It certainly isn't easy to see why the black king is worse placed on e1 than f1. Were it White to move here then the position would be a draw.”

John Nunn is a director of Gambit Publications, a leading chess book publisher. They have some interesting new books out this year.

Fundamental Chess Tactics by Antonio Gude: Once a player has learned how the pieces move, the next task is to put them to work – that is, to study tactics. For all players, from beginners to champions, tactical skill is the main component of chess ability. And this skill must be constantly practised and improved.

This book provides a systematic course in chess tactics and hundreds of exercises to sharpen and measure your skills. With Antonio Gude’s assistance, you will understand how the pieces work, so you can carry out your strategic plans and launch devastating attacks. And even in those games where things go wrong, you will always be ready to pounce when given the chance. The book is packed with entertaining and inspiring examples, brought to life with information and stories about some of the more notable figures in chess history.

Antonio Gude is a well-known chess writer and teacher from Spain who has represented his country in international correspondence chess events. His previous book for Gambit, Fundamental Checkmates, was shortlisted for the English Chess Federation Book of the Year Award.

125 Chess Opening Surprises: Surprising the opponent is a primary aim of modern opening preparation. You can’t afford to be a stationary target – gone are the days when players worked out an elaborate repertoire from which they never varied.

These 125 opening surprises land like bombshells in the apparent calm of standard openings and disorientate your opponents as they grapple with original problems. This book is a treasure-trove of unusual ideas at an early stage of the opening, each with a firm logical foundation, yet running against the grain of conventional play. Each idea has quick-strike potential and is supported by enough concrete analysis to enable you to try it with confidence.