ChessBase 2015 New Year's Puzzle Contest

We trust that you have enjoyed solving our 2014 Christmas puzzles, which were published from December 25 to 31. If you were meditating in a cave in the Hindu Kush mountains during that week and missed them, do not worry: you can review the problems by clicking on the images below, which will take you to specific installments.

December 25	December 26	December 27	December 28
December 29	December 30	December 31	January 1

Now to our puzzle challenge. We give you three full weeks to solve the following problems – and perhaps win a very nice prize. This will consist of recent ChessBase software, with autographs of top players – at least one a World Champion or ex. And the first prize will probably come with a personal dedication. Note that we have selected puzzles that are not easily accessible to computer solving. What is the point in giving positions that modern chess engines solve in their first seconds of thought? Note too that by some freak accident of the Universe all three problems were provided to us by puzzle king John Nunn.

This is a picture from 1983 of John Nunn composing a problem in my living room during a visit in Germany. Today, over 31 years later, he still supplies my family with chess and mind sport puzzles.

Puzzle one: How can it be a draw?

This is a nice little problem I received from John in 2001. It is one of those typical Nunn things that require no diagram to formulate:

White has a king, a queen and two pawns against Black's bare king.
It is White to move, but he cannot force a win. The game is drawn.

Can you reconstruct the position? The problem has an additional stipulation "White is not stalemated". If it didn't the position on the right would be a possible solution.

Out of curiosity (and not as part of today's task) you may want to think about how much material White can have against the bare black king, be on the move and still not be able to win. Once again: White is not stalemated and can acutally make moves. Prepare to be surprised.

Puzzle two: en passant mate

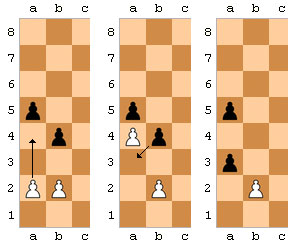Many years ago my sons were playing a game of chess against each other. Suddenly one came to me to complain that the other was cheating: "He wants to take a pawn from a square I didn't move it to!" I patiently explained to him that if a pawn moves two ranks forward from its starting position, and an enemy pawn could have captured it had the pawn moved only one square forward, then it can capture the pawn "en passant" (in passing), exactly as if the pawn had moved only one square forward and the enemy pawn had captured it normally. But it could only do so immediately after double-rank move was made.

The face of my son reminded me of the Prince George in the first 40 seconds of this Blackadder clip. "You are joking, right?" he said, and then, sarcastically: "This rule applies on every day of the week?"

The en passant rule was one of the last major changes in European chess, and occurred between 1200 and 1600. The motivation was to prevent the newly added two-square first move for pawns from allowing a pawn to evade capture by an enemy pawn.

And en passant capture occurs in a line of the French advicated by Steinitz (1.e4 e6 2.e5 d5 3.exd6 e.p.) and a main line of the Petroff (1.e4 e5 2.Nf3 Nf6 3.d4 exd4 4.e5 Ne4 5.Qxd4 d5 6.exd6 e.p.). It is also a popular motíf in chess compositions, as you have seen in our December 28 Smyllian puzzle.

Our New Year's puzzle is: What is the shortest game ending with an en passant capture and mate?

It is clear that both sides will be cooperating to bring about an en passant capture with mate. On our JavaScript board below you can play through examples of games ending on move ten, move nine and even move eight. Do you think a shorter sequence is possible, and if so what is the least number of moves required?

Puzzle three: A logical challenge

This puzzle was given to us – to family and friends, who spent an hour mulling over it – by John Nunn during a pre-Christmas visit this year. In the end a few of us solved it, but not without some fairly painful exertion of a few billion brain cells. The problem is as follows:

A hermit occupies one of six caves. Every day he randomly switches to an adjacent cave.
Every day we search one cave. Is there a strategy to ensure we will find him,
whatever switches he makes? How many times must we seach a cave?

To clarify: if the hermit is in cave one or six he is forced to move to cave two or five, which are next to them. In the four other caves he has two choices. We of course do not know in which cave he is when we start. Our search plan should discover him whatever he does – in fact he can even know our full search plan and still not avoid discovery.

The above is a what we used to solve the problem on the dinner table: six little wooden cups, with a stick to indicate where the hermit was hiding. You make a search plan, consisting of cave numbers (e.g. 1, 3, 5, 4, etc.) and then try to find a strategy for the hermit to circumvent it. A hint: I solved the problem by starting with three caves (2, 2 finds the hermit) and working my way up to six. Your answer should be a series of numbers indicating which caves you would search in which order.

I can tell you it was a very enjoyable dinner. Most enjoyable.

Bonus puzzle four

In case you cannot handle construction or logical problems we will include a final puzzle from our 2001 Christmas puzzle week:

In this picture you see a real child prodigy, one who started playing chess at an unusually early age. This chess prodigy went on to become a very strong grandmaster, one of the best in the world. Tell us who he is.

Send in your solutions

Please use the feedback form at the bottom of this page to submit your solutions. Do not forget to give your full (real) name, the town you live in and your email address – that is if you want to participate in our Christmas Puzzle Prize Contest. This requires that you have solved at least one of the puzzles on this page correctly.

Two winners will be chosen at random from all eligible submissions – we like to reward participation, not getting everything meticulously right. A third prize winner will be selected on the basis of the nicest message (in our opinion) that we receive. Closing date for all entries is January 21, 2015. Note that the arrival date will not influence the selection – so take your time.

And the prizes? They will consist of the most recent ChessBase software, with autographs of top players – at least one a World Champion or ex. And one of the prizes will have a personal dedication and the signatures of all the participants of the 2014 Zurich Chess Challenge – if nothing comes in the way of us getting them. Definitely worth a shot at winning, don't you think?