We begin with the selection of John's own compositions of chess problems and studies. If you missed them you may want to spend some time trying out solutions on our live diagram boards (where you can move pieces, retract moves and enter alernate lines). At the end you will find the solutions.
John Nunn, The Problemist 2006
In helpmates Black starts and helps White mate in the specified number of moves. In the above problem, for which John won third prize, we gave you a substantial hint: White pins his own rook on the first move, unpins it using the knight on the second move and uses the unpinned rook to mate on the third move. In the second solution the roles of the two white pieces are exactly reversed. Easy to solve now? Remember it is Black to play and help White to construct a mate of the black king in three moves.
John Nunn, The Problemist 24.10.2017
This recent problem won fifth prize. Two possible captures on a1 lead to the black rooks interfering with each other – in each case one rook blocks the other from making a vital capture.
John Nunn, British Chess Magazine 1984
If it were Black to move, then White could mate in 2, for example: 1...Kf4 2.Qe3+ Kg4 3.Qg3# or 1...d4 2.Qc5+ Ke6 (2...Kf4 3.Qf5#) 3. Bf5# But White has no move that simply maintains the situation.
John Nunn, The Problemist 2006
For this study John won first prize. We leave you to solve it without any hints. If you are at a loss you can fire up a chess engine, although the solution is not completely trivial for certain engines we know.
John Nunn, Secrets of Rook Endings, 1992
“The fact that Black is in zugzwang after White's first move is one of the most remarkable discoveries I made using an endgame tablebase,” John wrote in his book. “It certainly isn't easy to see why the black king is worse placed on e1 than f1. Were it White to move here then the position would be a draw.”
Solutions to the problems
Knight tours

During our trip to Cornwall we went on daily Nunn Walks, during which he gave us logical puzzles to solve. The first was fairly easy: “Suppose there is an ant on every square of a 7x9 chessboard, and at some moment all the ants crawl to an orthogonally adjacent square, that is left, right, up or down – but not diagonally. Prove that after this there must be at least one empty square.”
I got the answer in a few minutes: a 9x7 board has 63 squares; every ant moves from a black to a white square, or from white to black. But there is one less square of an individual colour – let us assume 32 black squares and 31 white. After crawling there must be 32 ants on white squares and 31 ants on black squares. So there must be a white square with (at least) two ants and a black square with no ants.
'The second problem was more difficult: Suppose you have a chessboard m squares up and n squares across. If m and n are both odd prove that a closed knight’s tour is impossible.
A “knight's tour” on the chessboard is a sequence of moves by a knight such that each square of the board is visited exactly once; a "closed tour” is one in which the square at the end of a knight's tour is a knight move away from the first square.
 After a closed knight tour on a regular board, or one that has an even number of squares, the knight will end on a square that is of a different colour to the one it started out from. On a board that has an odd number of squares, the number of squares of one colour is greater by one than the squares of the other colour. So if the knight can at all complete a tour it will end on a square of the same colour it started, and a closed tour is impossible. Try it out on a 5x3 board, using M&Ms or rice corns to mark the squares.
After a closed knight tour on a regular board, or one that has an even number of squares, the knight will end on a square that is of a different colour to the one it started out from. On a board that has an odd number of squares, the number of squares of one colour is greater by one than the squares of the other colour. So if the knight can at all complete a tour it will end on a square of the same colour it started, and a closed tour is impossible. Try it out on a 5x3 board, using M&Ms or rice corns to mark the squares.
Now to the final part of the problem: what if the board has an even number of squares, i.e. an m x n board in which m or n (or both) are even. We must find out for which values of m and n a closed knight's tour is possible. "I will give you the following information for free,” said John. "There is no closed knight’s tour on the small boards 3x6 and 3x8, but apart from these two special cases there is a simple rule to determine, given m and n (at least one even), whether there is a closed knight’s tour on an m by n board. What is it?”
I did not solve this – didn't even get close. So I will let John explain:
The answer to the knight’s tour problem about which m x n boards (at least one of m and n even) is that a knight’s tour is always possible, except if either m or n equals 1, 2 or 4. The only exceptions are the impossible small boards 3x6 and 3x8 mentioned in the question.
This is surprising because one would naturally expect that the wider the board, the easier it is to arrange a knight’s tour. However, all the 3xn boards are possible (for n even, n at least 10) but none of the 4xn boards.
It’s obvious that the 1xn and 2xn boards are impossible: on a 1xn board you have no moves at all, while on a 2xn board you cannot change direction. There’s a neat proof that the 4xn boards are impossible. Colour the board in the following way:
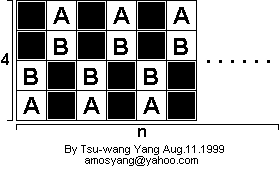
Suppose there is a closed knight’s tour. Then from each of the A-squares, the only legal moves are to a B-square. So all the moves from an A-square go to a B-square, and all the moves to an A-square come from a B-square. Since there is an equal number of A and B squares, it follows that these moves account for all the moves to and from B-squares. The upshot is that once you are on an A or B square, you will always be on an A or B square. Thus the squares coloured black in the above diagram will never be visited. So there is in fact no closed knight’s tour.
The proof that all the other boards are possible is more complicated and the details may be found at this comprehensive Knight's Tours page (from which the above image is taken).
I also failed on the 33 rooks problem, as did most of our readers: is possible to place 32 rooks on the standard 8x8 chessboard so that whenever you choose five rooks, at least two must be attacking one another? Easy: just fill the first four ranks, after which any selection of five rooks must include two on the same rank, and these will be attacking one another. “Indeed”, said John, “but now suppose there are 33 rooks on the chessboard. Can you prove that however they are arranged, it is always possible to find five rooks such that no two are attacking each other. There is a simple proof.” Once again I used M&Ms on a chessboard, but had to concede defeat. The problem is "simple” only in John's understanding for the term. His solution:
First let us number the squares on the board as follows:

There are only eight different numbers, so if there are 33 rooks then five of them must lie on squares with the same number. These five then don’t attack each other.
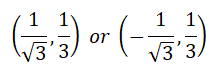 Finally the math problem: Consider the parabola of equation y=x^2. The normal is constructed at a variable point P and meets the parabola again in Q. Determine the location of P for which the arc length along the parabola between P and Q is minimized. The correct answer is that the arc length is minimised when P is one of the points shown on the right. Joshua Green of the USA solved this (and most of the other problems). He gets the personally dedicated copy of John Nunn's classic “Solving in Style”.
Finally the math problem: Consider the parabola of equation y=x^2. The normal is constructed at a variable point P and meets the parabola again in Q. Determine the location of P for which the arc length along the parabola between P and Q is minimized. The correct answer is that the arc length is minimised when P is one of the points shown on the right. Joshua Green of the USA solved this (and most of the other problems). He gets the personally dedicated copy of John Nunn's classic “Solving in Style”.
John Nunn is a director of Gambit Publications, a leading chess book publisher. They have some interesting new books out this year.
 Fundamental Chess Tactics by Antonio Gude: Once a player has learned how the pieces move, the next task is to put them to work – that is, to study tactics. For all players, from beginners to champions, tactical skill is the main component of chess ability. And this skill must be constantly practised and improved.
Fundamental Chess Tactics by Antonio Gude: Once a player has learned how the pieces move, the next task is to put them to work – that is, to study tactics. For all players, from beginners to champions, tactical skill is the main component of chess ability. And this skill must be constantly practised and improved.
This book provides a systematic course in chess tactics and hundreds of exercises to sharpen and measure your skills. With Antonio Gude’s assistance, you will understand how the pieces work, so you can carry out your strategic plans and launch devastating attacks. And even in those games where things go wrong, you will always be ready to pounce when given the chance. The book is packed with entertaining and inspiring examples, brought to life with information and stories about some of the more notable figures in chess history.
Antonio Gude is a well-known chess writer and teacher from Spain who has represented his country in international correspondence chess events. His previous book for Gambit, Fundamental Checkmates, was shortlisted for the English Chess Federation Book of the Year Award.
 125 Chess Opening Surprises: Surprising the opponent is a primary aim of modern opening preparation. You can’t afford to be a stationary target – gone are the days when players worked out an elaborate repertoire from which they never varied.
125 Chess Opening Surprises: Surprising the opponent is a primary aim of modern opening preparation. You can’t afford to be a stationary target – gone are the days when players worked out an elaborate repertoire from which they never varied.
These 125 opening surprises land like bombshells in the apparent calm of standard openings and disorientate your opponents as they grapple with original problems. This book is a treasure-trove of unusual ideas at an early stage of the opening, each with a firm logical foundation, yet running against the grain of conventional play. Each idea has quick-strike potential and is supported by enough concrete analysis to enable you to try it with confidence.





















 After a closed knight tour on a regular board, or one that has an even number of squares, the knight will end on a square that is of a different colour to the one it started out from. On a board that has an odd number of squares, the number of squares of one colour is greater by one than the squares of the other colour. So if the knight can at all complete a tour it will end on a square of the same colour it started, and a closed tour is impossible. Try it out on a 5x3 board, using M&Ms or rice corns to mark the squares.
After a closed knight tour on a regular board, or one that has an even number of squares, the knight will end on a square that is of a different colour to the one it started out from. On a board that has an odd number of squares, the number of squares of one colour is greater by one than the squares of the other colour. So if the knight can at all complete a tour it will end on a square of the same colour it started, and a closed tour is impossible. Try it out on a 5x3 board, using M&Ms or rice corns to mark the squares.


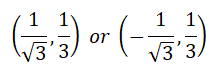 Finally the math problem: Consider the parabola of equation y=x^2. The normal is constructed at a variable point P and meets the parabola again in Q. Determine the location of P for which the arc length along the parabola between P and Q is minimized. The correct answer is that the arc length is minimised when P is one of the points shown on the right. Joshua Green of the USA solved this (and most of the other problems). He gets the personally dedicated copy of John Nunn's classic “
Finally the math problem: Consider the parabola of equation y=x^2. The normal is constructed at a variable point P and meets the parabola again in Q. Determine the location of P for which the arc length along the parabola between P and Q is minimized. The correct answer is that the arc length is minimised when P is one of the points shown on the right. Joshua Green of the USA solved this (and most of the other problems). He gets the personally dedicated copy of John Nunn's classic “







