ChessBase 17 - Mega package - Edition 2024
It is the program of choice for anyone who loves the game and wants to know more about it. Start your personal success story with ChessBase and enjoy the game even more.
For mathematicians, physicists, astronomers and any scientist that uses pure mathematics in their day-to-day work, Leonhard Euler is nothing but a legend. Born in Basel in 1707, Euler was one of the two greatest mathematicians of the 18th century. The other great from that era was Joseph-Louis Lagrange, who made great contributions from the analytic-method viewpoint. Euler's productivity is nevertheless unparalleled.
The Swiss 'Renaissance man' spent most of his adult life in Saint Petersburg and Berlin, where he developed most of his work, now collected in 92 volumes — or over thirty thousand pages! In the review of a collection of correspondence among eighteenth-century mathematicians, Gugliemo Libri reproduces what Pierre-Simon Laplace never ceased to advise younger colleagues: "Lisez Euler, lisez Euler, c'est notre maître à tous". ("Read Euler, read Euler, he is our master in everything"). [Better translated as "Read Euler, read Euler, he is the master of us all" - Ed.]
Euler's biography was marked by his dedication to scientific progress. In 1735, he lost the sight of one eye, while in the 1760s a cataract in his remaining good eye meant he would spend the rest of his life in total blindness (he passed away in 1783). The tragedy did not diminish his productivity, however, as his mental calculation skills and extraordinary memory remained intact.
He made contributions in a wide set of fields, including music and chess. In his "Solution d'une question curieuse qui ne paroit soumise a aucune analyse" (Solution of a curious question that does not seem to have been subject to any analysis), he tackles the following problem:
I found myself one day in a company where, on the occasion of a game of chess, someone proposed this question: To move with a knight through all the squares of a chess board, without ever moving two times to the same square, and beginning with a given square.
Although this problem had been presented and partially solved by Eastern thinkers, like Ali Bin Mani and Abu-Bakr Muhammad b.Yahya as-Suli, the first comprehensive mathematical analysis of the Knight's Tour was presented by Euler.
Master Class Vol.9: Paul Morphy
Learn about one of the greatest geniuses in the history of chess! Paul Morphy's career (1837-1884) lasted only a few years and yet he managed to defeat the best chess players of his time.
In an article from almost exactly a year ago, Frederic Friedel retold the story of Xaver, a nine-year-old boy who was able to complete a Knight's Tour blindfolded and from any starting square. A concise explanation of the basic elements of this sequence was presented there.
The "Knight's Tour" of the chessboard was first proposed (solved) in a ninth century Arabic manuscript by Abu Zakariya Yahya ben Ibrahim al-Hakim. The author gives two tours, one by Ali C. Mani, an otherwise unknown chess player, and the other by al-Adli ar-Rumi, who flourished around 840 and is known to have written a book on Shatranj (the form of chess then popular).
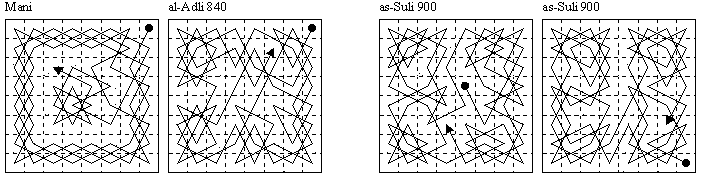
A "closed tour" is one in which the square at the end of a Knight's Tour is a knight move away from the first square, as in the second example above. The master of Shatranj as-Suli, who based his works on those of al-Adli (which he criticised), published the two closed tours given above on the right. The first example shows perfect axial symmetry on the left half-board, the second is composed of two quasi-symmetrical half-board tours.
Incidentally the number of possible knight's tours on an 8x8 board is surprisingly large — estimates range between 13 and 33 trillion. And much more on bigger boards. Here, for curiosity’s sake, is a Knight Tour on a 130x130 board.
As Ed Sandifer states in his paper How Euler did it, "Knight’s Tours are closely related to a kind of magic square called 'pandiagonal', and Euler wrote about pandiagonal magic
squares in 1779, when he wrote 'Recherches sur un nouvelle espèce de quarrés magiques' (Researches on a new kind of magic squares)".
However, as George Jelliss points out in his extensive recap of everything related to the study of Knight's Tours, Euler did not compose any 'Magic Knight's Tours' as has been stated repeatedly.
What Euler did manage to contribute during his brief exploration of this subject was a general method of completing partial tours and deriving new tours from existing solutions. He also explored symmetries and solved tours in smaller boards. The Swiss mathematician also gives the first-ever examples of tours exhibiting quaternary symmetry — i.e. two tours of cross-shaped boards in which the symmetry is achieved by reflection in the two diagonals.
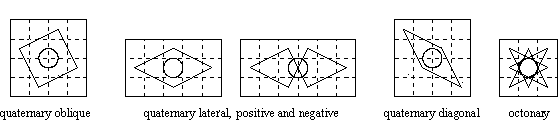
Quaternary symmetry
The study of these problems and the story behind how they were solved throughout the years are subjects that can be scrutinized in-depth. If you are interested, Jelliss' web page is a great starting point. The fact that a man of Euler's stature considered this question as worthy of consideration shows the extent of the influence chess had in science and culture in general. We hope it serves as inspiration to delve into the rich and fertile history of our beloved royal game.
