Elo Rating System: how underrated are the kids?

Age and the Elo Rating System, how underrated are the kids?

By Ganesh Viswanath

An interesting phenomenon of the ELO rating system is that when examining game outcomes for a group of lower rated players, higher rated players tend to under-perform relative to the theoretical ELO probability, and lower-rated players over-perform. This begs the question, what are the causal factors in explaining the inability of the ELO system to predict results? I hypothesize that age is the key factor and that most of the discrepancy between the theory and the data can be explained by underrated juniors.

The ELO system and its discrepancies has been well documented in the past. It was not too long ago that a ratings conference was held in Athens (1) to discuss the future of the rating system, and various issues were brought up such as ratings inflation, the optimal K factor and other statistical concerns. As a primer for those unfamiliar with the rating system, the ELO is a statistical based system for ranking players. The original ELO formula proposes that a player who is 100 points higher rated should win a game with a 64% probability, and a 200 point difference gives approximately a 75% chance of winning for the higher rated opponent. A key assumption of ELO is that players’ abilities are normally distributed (2). By this assumption, the expected probability of winning follows the following logistic curve, illustrated in Figure 1.

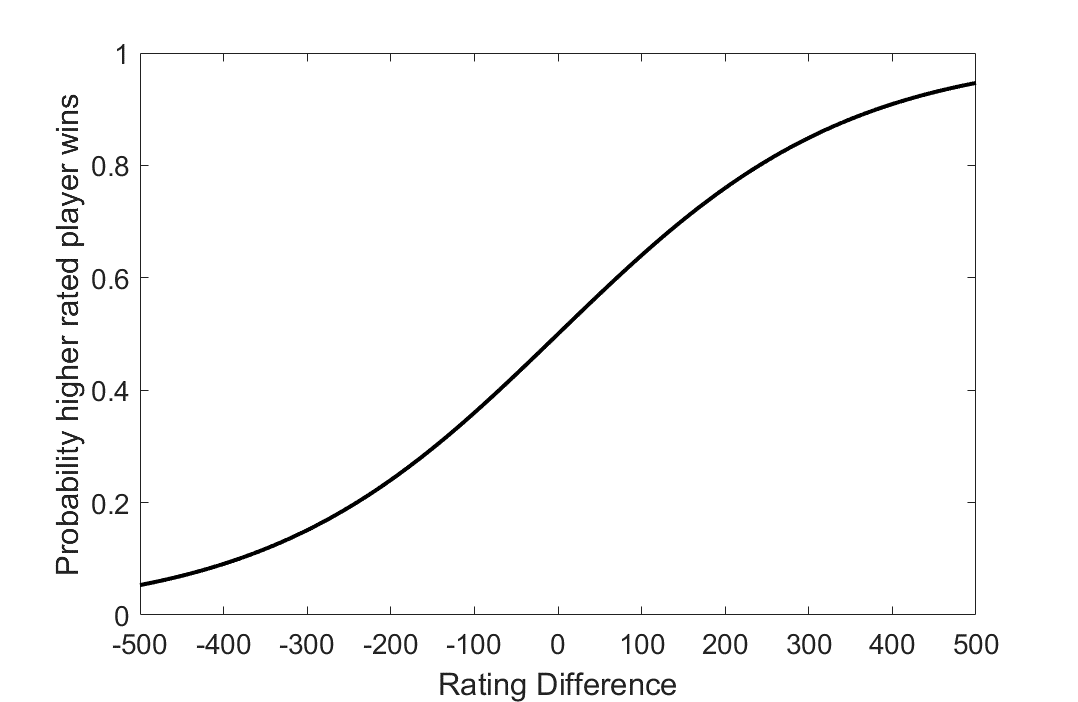
Figure 1: Theoretical ELO curve

A result established in a previous article by chess statistician Jeff Sonas (3) is that there are significant discrepancies between the implied probabilities of the ELO system and the data. How does one measure these discrepancies? A simple way is to compile a database of game results and player ratings, which I have done using Chessbase’s MegaBase 2016. Based on this sample I can estimate a conditional expectation function, which is the average score players are making at each rating difference. For example, if there are 100 games in my sample with a rating difference of 100 points, and the higher rated player scores 60/100, then the sample estimate of the expected score of the higher rated player is 0.6. Using this procedure, I look at a cohort of players born in the 1970s and subdivide the group into players at grandmaster level (rated >2500), an experts to master level (rated between 2000 and 2500), and sub-expert players with a rating between 1500 and 2000. The results of this exercise, shown in Figure 1, illustrate that it is clear the ELO system works well for the higher rating groups, however there is essentially more noise in the lower rating group, with evidence that lower rated players are performing above the expected score given by the ELO system, and higher rated players are underperforming. This begs the question, what are the causal factors in explaining this discrepancy in the rating system for the lower rated group? Is it just noise or is there a more compelling explanation?

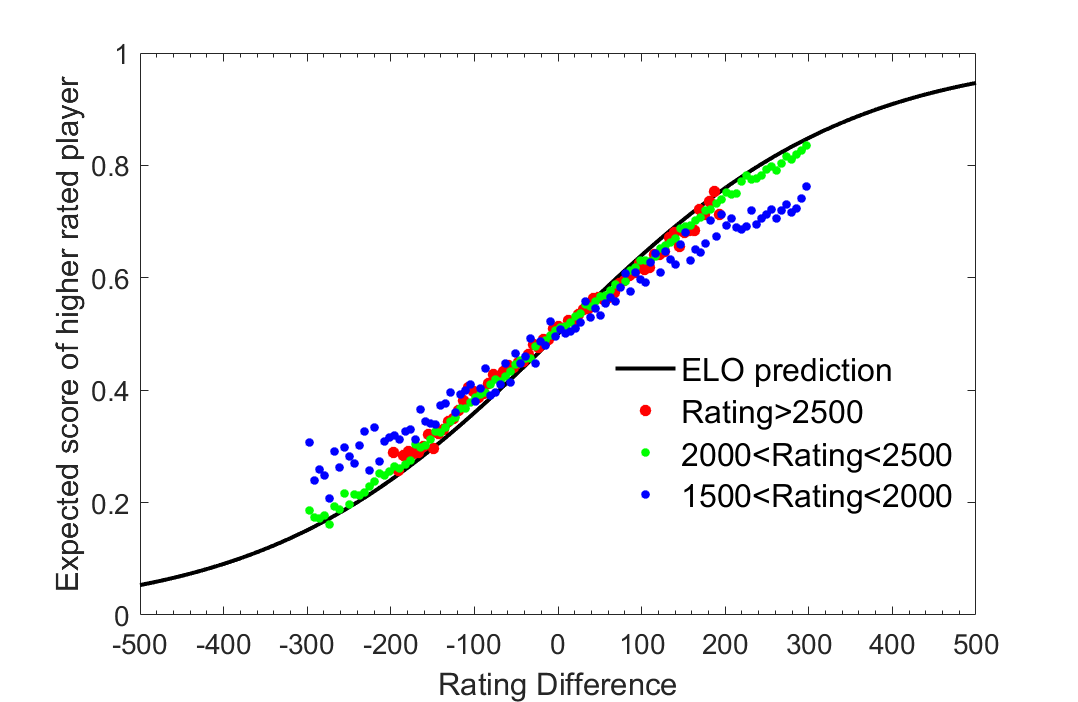
Figure 2: Comparing sample distribution of results for different rating groups
I hypothesize that what really drives this discrepancy is the systematic undervaluation of young players. This is intuitive as we all know that young players are often underrated and their current ratings might lag their true potential by a significant margin. The ELO system works great in a perfect world where all players have transitioned to their “steady-state” ratings, however if there are vast discrepancies between realized and true rating ability then this can explain the trends we are seeing in the data. First, I examine the game results of all current juniors (4), and divide the sample into those that are currently under 2000 and a 2000+ category (Figure 3 ). Systematic undervaluation of lower rated players is evident in both samples indicating that it is a junior-wide phenomenon. It is startling to note how extensive the undervaluation of the younger player is. Lower rated juniors are getting an expected score 10 percentage points more per game than implied by the ELO rating system. This result is intuitive when we think of how juniors who are at master level strength today have clearly overperformed their ratings in order to get to their current level.

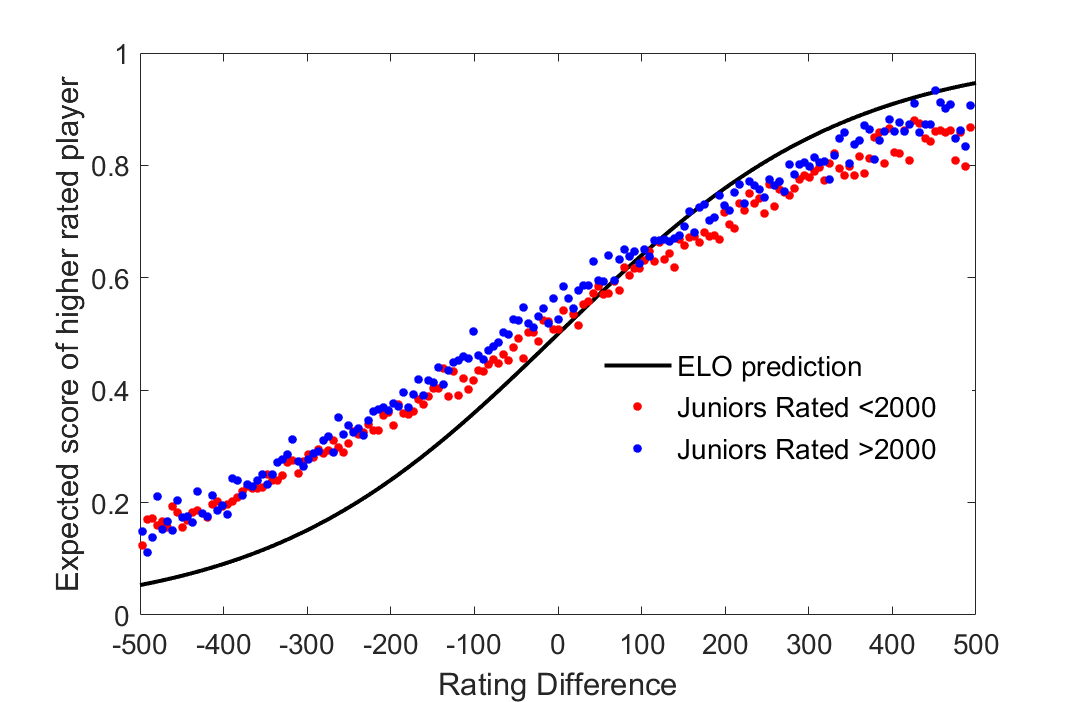
Figure 3: Undervaluation of lower rated players is a youth phenomenon

To further establish my reasoning I compare the current under 2000 rated sample of junior players to the game results of adult players from the same rating group who belong to a cohort born in the 1970s (Figure 4). As I suspected, the adults tend to perform in accordance with the ELO system when they are lower rated, however are more likely to underperform than juniors when they are higher rated than their opponents.

What are the implications of this result? Ratings statisticians recognize that younger players are often more likely to improve and transition to a higher rating. Both FIDE and the USCF give higher K factors (5) to younger players so they can converge to their steady state faster. However, this still does not solve the intrinsic problem of ratings undervaluation that we see in the data. One of the potential costs of the system is that it is implicitly penalizing adult players that are having to face many juniors and are continually losing rating points due to their under-performance relative to the ELO system. One potential solution would be a recalibration of the parameters of the current ELO formula for predicing probabilities, and in particular controlling for age.

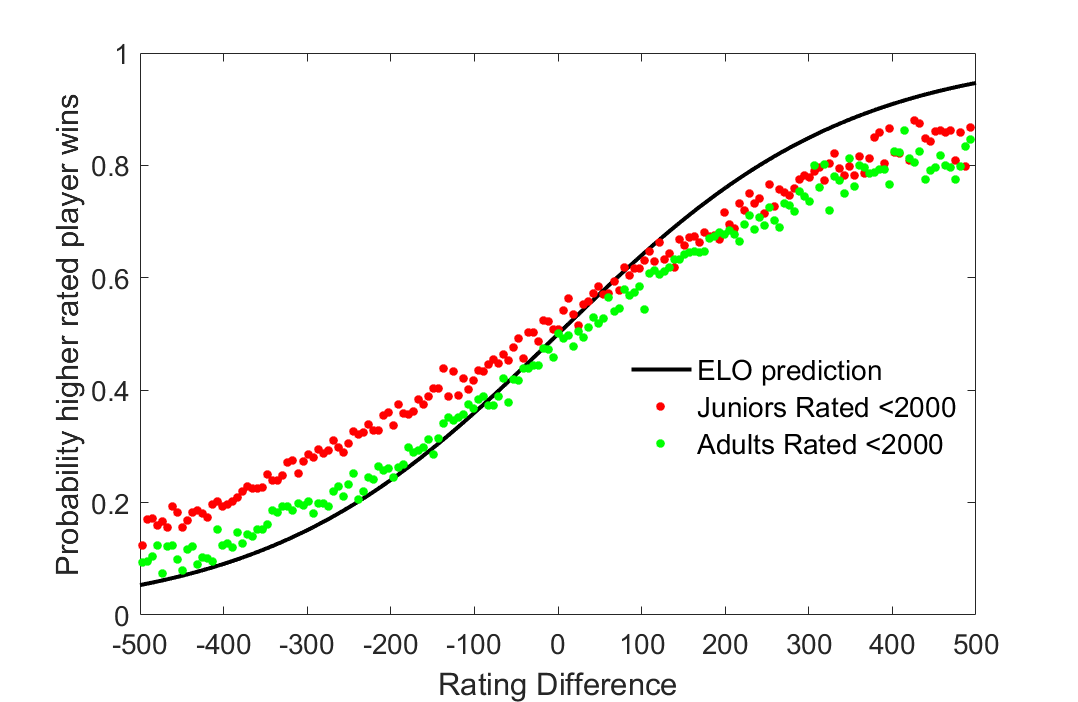
Figure 4: Comparing Under 2000 juniors to adults at a comparative rating level

My work in this article is by no means complete and there are further robustness checks and data analysis needed to support my conclusion that underrated youth are the driving force behind rating discrepancies. The next step in my analysis would be to extend my sample size and track junior-junior, junior-adult and adult-adult pairings more accurately to demonstrate that all of the rating discrepancy is being driven by games involving juniors. My motivation in writing this article is to shed light on what is an understudied issue in chess statistics and is increasingly relevant when we see the rise of chess as being a game of youth with an increasing share of young players in the modern game.

I would like to acknowledge the assistance of Jeff Sonas in starting the data collection for this project, and Jonas Tungodden for feedback.

Notes

(1) http://en.chessbase.com/post/impreions-from-fide-rating-conference-2010

(2) Although this is not the subject of this article, there are arguments against the validity of the normality assumption.

(3) See article by Jeff Sonas at http://en.chessbase.com/post/sonas-overall-review-of-the-fide-rating-system-220813

(4) All players registered in the player encyclopedia of MegaBase 2016, born on 1st of January, 1998 or later

(5) K factors determine how many points a player can win/lose from a game. The rating change is equal to Kfactor (Game outcome-expected winning score). For example, if you are 100 points higher rated you should win 64% of the time according to the ELO system so the expected winning score is 0.64.

About the author Ganesh Viswanath is from Perth, Australia and is currently studying a PhD in economics from the University of California, Berkeley. In his spare time he likes to play chess tournaments in the bay area (facing a lot of juniors!) and has more recently been trying to venture into chess statistics.