Elo oddities: the tortoise and the hare

Elo oddities: the tortoise and the hare

Chinese GM Li Chao recently rejoined the 2700 club after winning 5.6 Elo from his 9.0/9 victory at the 5th Colombo International Chess Festival 2012. While nine in nine sounded impressive, the results page showed something quite odd: the Chinese player had a 2622 performance, considerably below his 2693 rating. Six of the eight rated opponents had ratings under 2000 and one was even rated 1405. In spite of this he had still managed to gain 5.6 Elo. How was that possible?

The reason is that today games are rated individually, and any player rated 400 Elo or more below your rating will still yield 0.8 Elo. At a time when the minimum FIDE rating was 2200 the greatest disparity possible was around 600 Elo, but now games with a full 1400 Elo difference could take place. Could this be the source of ratings inflation? Perhaps Magnus Carlsen could find a much easier way to break Garry Kasparov’s record: win a few very weak opens, and presto! He would be the new record holder, even if he did not play a single opponent within a thousand Elo of his rating.

In order to get to the truth of the matter, experts and mathematicians Jeff Sonas, John Nunn, and Ken Thompson were consulted and held a dialogue between themselves which we publish here.

Jeff Sonas, Statistician and creator of Chessmetrics, was the first to reply.

My understanding is that this rule was introduced for political reasons long ago, purportedly to give top players some incentive to play in open events.  When FIDE proposed raising the cutoff from 350 points to 400 points a couple of years ago, and asked for my opinion, I agreed that it was a change in the right direction, and stated that it would be even better to go up to 500 instead. I have since changed my opinion on this, and decided we either should get rid of the rule altogether, or make it an "800-point rule" instead. You can see my most recent analysis from a year ago I discuss the 400-point rule amongst the two graphs that have large blue rectangle outlines, about halfway down.

There is a statistical rationale for the rule to some degree, since the chaotic nature of chess (and the variability of ratings) means you can never really be 100% sure that one player will beat another, and rarely can you even be 99% sure. It is certainly not a "guarantee" to score 100% in a whole event. For one thing, it is quite possible that opponents paired against the tournament leader in a late round of a Swiss would have done better than expected and in fact would be stronger than their pre-tournament rating would indicate.  I think an 8.5/9 score for Li Chao in such an event would be a reasonable prediction, and would not have resulted in a single point of Elo gain for him.

But yes, if someone strong were able to organize lots of events like this, and the rating administrators looked the other way, a strong player would likely be able to boost their own rating a bit. I certainly don't think it has much to do with the increased ratings of top players, though, and the artificially high rating would sort itself out eventually because it would also artificially increase the player's predicted score and they would therefore struggle to maintain the artificially high rating.  In this way the Elo system is supposedly “self-correcting”, although I’m not sure this really works very rapidly when opponents’ ratings are at all inaccurate.

Ken Thompson, computer chess pioneer

I don’t think it makes a difference whether you pick a large number (say 400 or 800) and employ this rule. I don’t think that human-human interactions will accurately follow the normal curve beyond this point. Even if it is true that this difference can be milked for rating, there are several practical issues working against it. The player has to spend lots of silly time pounding on weak players to gain points. He has to continually keep vigilance to accomplish this. One mistake and he will lose many times what he has slowly gained. Once the player has amassed his 3800 Elo, what is he to do with it? Compete and give it to strong players? Sit on it and brag about being on the top of the rating lists? I don’t think this is a cause of inflation since the weaker player loses as many points as the stronger player gains, i.e. zero sum, no inflation.

John Nunn, Grandmaster, mathematician

This rule was introduced for a simple reason: to prevent players losing Elo points by winning a game. If one player in a tournament is rated far below the others, then including that player can lower the average rating of your opponents by so much that your expected score is increased by more than one point. Then beating that player will leave you worse off than if you had not played him at all. This is not just an academic situation. For very strong players it could easily happen in cases where, for example, a strong tournament includes a 'local player' who is much weaker than the others, or in Olympiads where your first round opponent was relatively weak.

In recent years there have been a few cases in which relatively well-known GMs have apparently attempted to exploit this rule by playing in very weak tournaments. However, in these cases the player concerned only appears to have gained a few points (less than five). Of course, by doing the same thing over and over again a player could artificially boost his rating, but it would be very time-consuming.

Jeff Sonas (to John Nunn)

It seems to me that the scenario you describe (wanting to avoid a victory over a low-rated player causing you to lose rating points) motivated the rule to calculate rating change on a game-by-game basis instead of using average opponent rating for an event. It also motivates the related tiebreak rule that might calculate performance rating after first removing the lowest-rated opponent, where we don't want to penalize someone's performance rating due to a win against a very weak player.

However, I don't see how capping the expected score at 89% would prevent players losing Elo points due to a win.  As long as you are calculating rating change on a game-by-game basis, even with an expected score of 99% or 100% you would still never lose rating points from a win.

John Nunn (to Jeff Sonas)

The original rating rules had no 350-point rule. It must be remembered that in 1970 the rating list was very small and it was never envisaged that it would be extended substantially. Only top tournaments were rated (and these were invariably all-play-all events) and all calculations were done by hand. The 'Losing Rating Points For Winning A Game' problem didn't really arise. The top players always skipped the first round or two of an Olympiad, and in any case any weak opponents would be unrated, so the games simply didn't count.

But times changed, the rating list expanded and started including more and more weaker players. Open tournaments appeared, and the LRPFWAG problem started to become significant. I don't remember exactly when the 350-point rule was introduced to deal with this, but I believe it was around 1980. Later, in 1988 or 1989, Karpov was unhappy about losing points when he had won a tournament, arguing that the aim of taking part in a tournament was to win it, and if you have achieved that then you shouldn't lose points through not having won by a large margin. For a time the 'Karpov rule' was in effect, that you couldn't lose points for winning an event. This was later scrapped.

Rating games individually is a fairly recent innovation, and for the vast bulk of the lifetime of the Elo system it was done on a tournament basis (because it made the calculations easier, especially for all-play-all events). The current rule is in a way a hangover from the earlier times, but I think there is some logic in it, although one can argue over the exact details. Rapidly improving young players, for example, can be massively underrated.

What to make of all of this? To start with, one must reiterate Ken Thompson’s point that it is ultimately a zero-sum game. In other words, even if a 2700 player can win Elo by beating rank beginners, those beginners will also lose the same corresponding Elo. So, does this mean all is okay? Sort of.

As explained by Jeff Sonas if the purpose is to prevent a player from losing Elo because he won a game, then rating each game individually solves this even without a ratings cap. The artificial 400 Elo cap just means that the FIDE rating system will always consider that any player rated at least 1400 never has worse than an 8% chance against another player whether he be Magnus Carlsen, Garry Kasparov, or Bobby Fischer. We beg to disagree.

Still, does that mean there is no inflation? Perhaps, perhaps not. Jeff Sonas explained:

In my opinion the main source of inflation is that newly rated players are receiving ratings that on average are too high, which is basically injecting rating points into the pool. This is possibly because rated players take it easy on unrated players in their games, and the unrated players therefore are showing an artificially high performance rating in those games. I have demonstrated through simulation that over a few years, these excess rating points (despite appearing only in new players) will gradually propagate through the entire rating pool, eventually reaching the very top.  I believe this to be one possible explanation for the effect seen in the following graph:

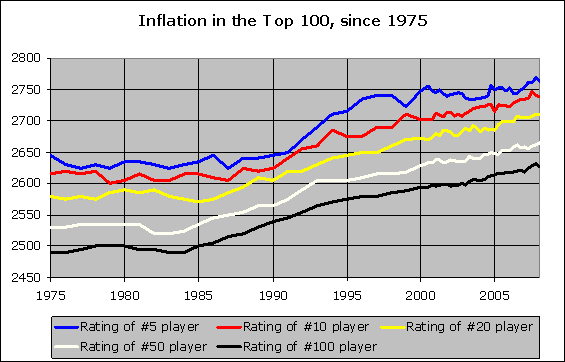
(taken from Rating inflation – its causes and possible cures)

If excess rating points were appearing at the bottom of the pool, and slowly distributing around, you would eventually see the rating of the #100 player (whoever that may be) go up, then the #50 player, and finally (maybe even years later) the #10 or #5 player.  As I said, I have demonstrated in FIDE meetings that a more aggressive (or more conservative) formula for new player ratings will ultimately raise (or lower) everyone’s rating, depending on players’ connectivity within the rating pool.  So a zero-sum operation will eventually settle down to become non-inflationary, I believe.  Within reason.  I certainly don’t think the “350 point rule” or “400 point rule” explains all of the 2800+ ratings and 2700+ ratings we are seeing; I think it is far more likely that it comes from new players’ initial ratings.

Copyright ChessBase