Computer predictions, simulations and scenarios
By James Jorasch and Chris Capobianco
Sometimes threats and opportunities remain hidden in plain view because something much more captivating is holding a viewer’s attention. The thought of tiebreaks, for example, isn’t nearly as thrilling as watching the unfolding Candidates’ Tournament games. Let’s take a look at why that’s problematic.
With his loss against Anand, Aronian now needs to make up half a point to catch up with the two leaders. But our simulations show Aronian dropping from a 36.2% chance to win the tournament down to 16.8%. Why such a large drop? The answer lies buried in the tiebreak rules. These rules can have a significant effect on the outcome in the tournament.
The tiebreaks are applied in this order: head-to-head results, number of wins, Sonneborn-Berger score, rapid game match, blitz game match, and finally an Armageddon game. Our simulation software has all of the rules built in, so we can track exactly how many ties are broken by each tiebreak rule in a given simulation run.
Let’s take the example of Anand and Aronian. Aronian is only a half point behind Anand, but catching up isn’t going to help him if the tournament ends in a tie between Anand and Aronian. In that case, Anand would have a 1.5 to 0.5 record against Aronian and would thus eliminate Aronian in the head-to-head tiebreaker. The net effect is that Aronian probably needs to make up a full point between himself and Anand. This is one of the reasons that Aronian drops from 36.2% to to 16.8% in the latest simulation. In effect, Anand’s win over Aronian was worth not 1 point, but 1.25 points, under these tiebreak conditions.
For this reason, we call games between the tournament leaders with this tiebreak structure “Power Games”. You can see the upcoming schedule of Power Games in GM Jon Speelman’s update.
As a demonstration of the importance of Power Games, see below for simulation results of the round ten game between Caruana and Anand.
Win probabilities after round nine
| |
After Rd 5 |
After Rd 6 |
After Rd 7 |
After Rd 8 |
After Rd 9 (vs Rd 8) |
Point Standings |
| Anand |
5.5% |
9.4% |
11.0% |
11.4% |
26.6% (+15.3%) |
5.5 |
| Aronian |
26.8% |
40.1% |
42.2% |
36.2% |
16.8% (-19.4%) |
5.0 |
| Caruana |
16.9% |
10.8% |
10.5% |
20.2% |
20.8% (+0.6%) |
5.0 |
| Giri |
10.4% |
8.7% |
6.8% |
5.7% |
4.1% (-1.6%) |
4.5 |
| Karjakin |
28.0% |
27.2% |
25.1% |
25.3% |
31.0% (+5.7%) |
5.5 |
| Nakamura |
5.3% |
1.3% |
2.9% |
0.5% |
0.1% (-0.4%) |
3.5 |
| Svidler |
5.5% |
1.7% |
1.4% |
0.7% |
0.6% (-0.1%) |
4.0 |
| Topalov |
1.7% |
0.9% |
0.2% |
0.1% |
0.0% (-0.1%) |
3.0 |
Anand moves up to 26.6%, but still trails Karjakin, who is in the lead with 31.0% in our simulations.
Three players now combine for a less than one percent chance of winning the tournament: Nakamura, Svidler, and Topalov. While they only have a small chance of winning the tournament, they could still have a huge impact in any game by beating one of the leaders.

Giri’s tense and complicated battle with Caruana ended with his ninth draw in a row as his chances in our simulation fell from 5.7% to 4.1%.

The top four players have now formed a close pack with just 15% separating the probability of their winning the tournament.
Simulations of Research Scenarios for Anand
With Anand joining the lead, these simulations look at a few scenarios for him over the remaining rounds.
| |
Sim 1 |
Sim 2 |
Sim 3 |
Sim 4 |
Sim 5 |
| Rd 10 Caruana-Anand |
Draw |
Draw |
Draw |
Win |
Draw |
| Rd 11 Anand-Karjakin |
Draw |
Draw |
Win |
Draw |
Win |
| Rd 12 Nakamura-Anand |
Draw |
Win |
Draw |
Win |
Draw |
| Rd 13 Anand-Giri |
Draw |
Draw |
Draw |
Draw |
Draw |
| Rd 14 Svidler-Anand |
Draw |
Draw |
Draw |
Draw |
Win |
| Simulated Winning Chances |
18.7% |
60.8% |
85.4% |
89.7% |
97.7% |
Sim 1 illustrates Anand’s chances when he draws all the rest of his games. He ends up winning 18.7% of those tournaments. With just a single additional win, Anand increases his chances considerably, but note the difference between Sim 2 and Sim 3.
In Sim 2, he defeats Nakamura to rise to 60.8%. In Sim 3, he again has only one win, but it is in a Power Game against Karjakin and thus results in a bigger leap to 85.4% winning chances! Some of this gain is from taking down a leader, and some of it is the tiebreak benefits as mentioned above.
Sim 4 and Sim 5 illustrate two wins for Anand, with the Sim 5 win against Karjakin and Svidler virtually locking Anand into first place.
Quantifying a Power Game
Power Games are going to be a focal point in the remainder of the rounds. Anand won the Power Game of round nine, pushing Aronian’s chances of winning the tournament down to 16.8% in our simulations.
Round 10’s Power Game will be Caruana-Anand. The table below shows the results of three simulations, examining all three possible outcomes of the game and the effect on the winning chances of all tournament participants.
| |
After Round 9 |
Sim 1
Caruana Wins |
Sim 2
Draw |
Sim 3
Anand Wins |
| Anand |
26.6% |
6.3% |
31.1% |
56.2% |
| Aronian |
16.8% |
19.6% |
17.0% |
9.4% |
| Caruana |
20.8% |
42.5% |
13.3% |
2.1% |
| Giri |
4.1% |
3.2% |
4.6% |
3.9% |
| Karjakin |
31.0% |
27.6% |
33.3% |
28.0% |
| Nakamura |
0.1% |
0.1% |
0.1% |
0.1% |
| Svidler |
0.6% |
0.7% |
0.6% |
0.3% |
| Topalov |
0.0% |
0.0% |
0.0% |
0.0% |
A win by Caruana would put him in the driver’s seat with a tournament leading 42.5% winning chance, with Anand pushed down to 6.3%.
A draw benefits Anand (who moves up to 31.1%) since he has half a point more than Caruana in the current standings. Every round that he is not losing ground gets him closer to a win (though his head-to-head score against Karjakin could hurt him later). Conversely, the draw moves Caruana down to 13.3%.
A win by Anand moves his chances up to 56.2% in our simulation and brings Caruana down to 2.1%. This is clearly a Power Game that Caruana cannot afford to lose. Even if Caruana follows this loss with a win against Topalov in Round 11, his chances only rise from 2.1% up to 6.3%.
Tournament Analytics
All games of the Americans (Caruana and Nakamura) and Russians (Svidler and Karjakin) were drawn in Round 9, though Anand’s win improved Karjakin’s chances, so the Russians once again move upward relative to the Americans with a gap of more than 10%.

The expected winning score for the tournament moved lower this round to 8.56. The trend in the chart below shows the biggest gain in 8.5 (+3) as a winning score - happening 459,000 times (45.9%) in our simulation of a million tournaments.

The probability of a tie grows as Anand joins Karjakin in the lead. The number of tournaments expected to be decided in a tiebreaker is now 31.9%, up several percent over the 28.6% of round eight. Of those extra ties, the majority are being decided in the first head-to-head tiebreaker because of the Power Game results between Anand and Aronian and between Karjakin and Anand.

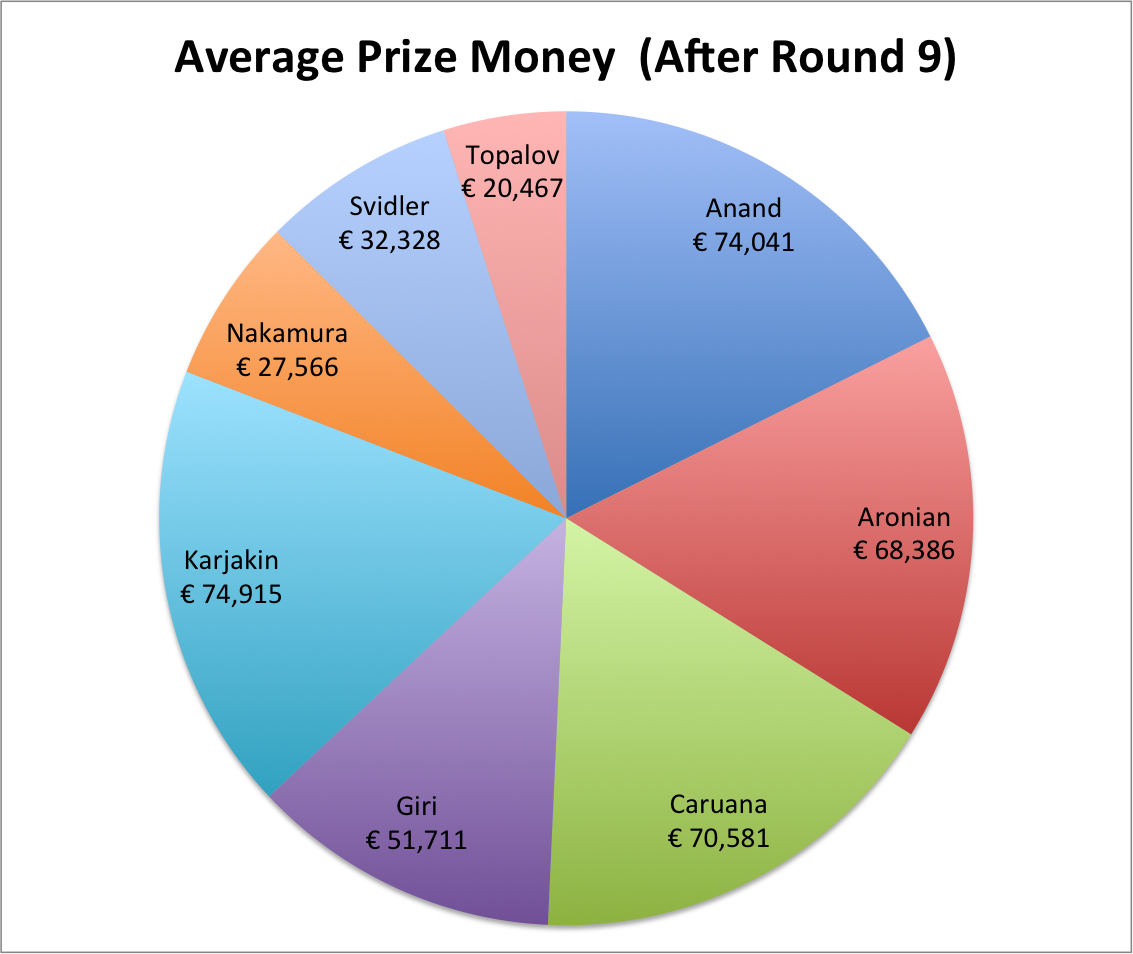
Money
The simulation tracks prize money earned by each participant at the conclusion of the event, so we show in the chart below what the players average over the million simulations. Note that this does not attempt to incorporate the extra value of winning first place in the form of the minimum prize money earned from the World Championship.
Anand adds a robust €13,400 to his expected prize money with his win over Aronian. Aronian drops €11,600 in simulated winnings.
Methodology Note
This report was created by running millions of simulations of the Candidates Tournament using our tournament software. We introduced this software the day before the tournament began. All actual game results to date are included in the simulation, and the remaining unplayed rounds are simulated based on a number of factors. This report discusses angles of interest on simulated tournament results and each player’s expected probability of winning.
|
About the authors |
 |
James Jorasch is the founder of Science House and an inventor named on more than 700 patents. He plays tournament chess, backgammon, Scrabble, and poker. He lives in Manhattan and is a member of the Marshall Chess Club. |
 |
Chris Capobianco is a software engineer at Google. He is a two-time finalist at the USA Memory Championships and has consulted on memory for finance, media, advertising and Fortune 500 companies such as Xerox and GE. |
If you have questions about tournament statistics that have not been covered, please get in touch. We’ll try to answer it in a future round report. Feel free to forward this along to friends. Interested in getting a copy of each round report? Send an email with the subject line “subscribe candidates tournament.”