.jpeg)
Winning starts with what you know
The new version 18 offers completely new possibilities for chess training and analysis: playing style analysis, search for strategic themes, access to 6 billion Lichess games, player preparation by matching Lichess games, download Chess.com games with built-in API, built-in cloud engine and much more.
Let me remind you: in this chess variant checks are illegal, unless it's checkmate. This means that you cannot make a checking move, even if it would stop the opponent's mate.
Checkless Chess – Helpmate in two
In the first position Black (who starts) needs to play 1.d1=R. White takes a queen: 1...a8=Q. And now comes the unusual mate: 2.Rf1 Qg2#. The black king cannot capture the queen or move to the e-file because that would expose the white king to a discovered check, which is illegal.
In the second position Black plays 1.d1=B and White plays 1...a1=N. There follows 2.Bb3 Nc6#. Black is mated since he cannot move his king off the a2-g8 diagonal. The bishop check would be illegal. Amazing, all four promotions with just four pieces.
Here are the solutions to the two Checkless Chess puzzles from our December 25 puzzle page:
The first two problems are by T.R. Dawson and were composed in 1927. 1946. Your task was to add a white queen in each diagram, on a legal square, and then stalemate Black in one move.
The solutions are +wQe1 and 1.f4 stalemate; +wQa1 and 1.a4 stalemate.
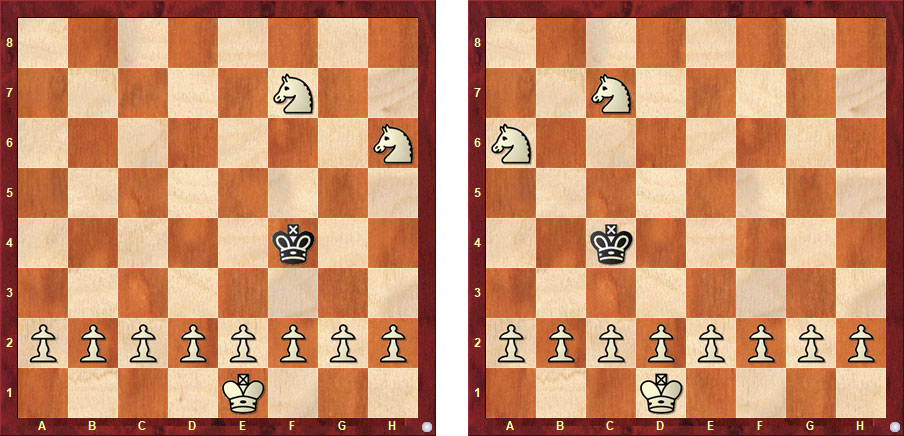
The second set is by Bengt Giöbel. Once again you have to add a white queen, but this time mate in one move.
The solutions are +wQc1 and 1.d3# and +wQa1 and 1.b3#.
In addition, you were asked to figure out why, in diagrams that are perfect mirror images, the solutions are quite different. The answer is that with all the white pawns on their original squares the white queen could not have crossed over the right side of the board. So it must always be placed to the left of the white king.
This is a problem by Rafael M. Kofman, published in Vecherny, Leningrad 1968, where it won the 3rd prize. You are required to replace the white king on the board and then mate in two moves.
Solution: add the white king on e1, and then 1.0-0-0! (threatening 2.Rd8#) 2.0-0 2.Rg1#.
The first position is a classic – it was composed by Bruno Sommer in 1910. White takes back his last move and plays something different, mating instead in one move. Solution: his last move was exf6 e.p. (Black has played ...f7-f5 before that). So with a white pawn on e5 (and a black pawn on f5) White delivers mated by playing 1.e8=Q#.
The second position is by Werner Keym, who provided me with a number of puzzles for the Christmas pages. It was published in 2010 and is the most economical form of this kind of retractor. White should take back his previous move and instead mate in two moves. Black is stalemated. Solution: White retracts the move 1.g2-g4 and plays 1.g2-g4. This makes the en passant capture legal, and Black is forced to play 1...hxg3 e.p. and White can play 2.hxg3 mate.
And finally a more recent retractor, a problem by J. Coakley, Chess Cafe 2014: White takes back his previous move and instead mates in one. This has the same theme as the two above, but is quite intricate.
Solution: White cannot castle in the problem position, because both f1 and g1 are attacked. But after taking back 1.bxc6 e.p. the pawns on b5 and c5 block the bishop diagonals. Now White can castle and mate: 1.O-O#.
In retractor problems, an en passant capture is allowed as backward or forward moves, unless they can be proven illegal.
The subject of our December 29 puzzle page was the selfmate. In this form of chess problem White must force Black to mate him, while the opponent will do everything he can to avoid that happening. We also included a (festive) self-stalemate that required White to stalemate himself against the will of Black. Here are the annotated solutions to replay:
That should suffice for the second day of a hopefully much better new year. I will publish the solution to our final Christmas Puzzle instalment on Monday. The train problem included there has been straining many minds around the world. I have 2700+ GMs begging for the solution, and a math professor, a quantum physicist, the head of a project group at Intel, and others still struggling. They have asked for some clarification:
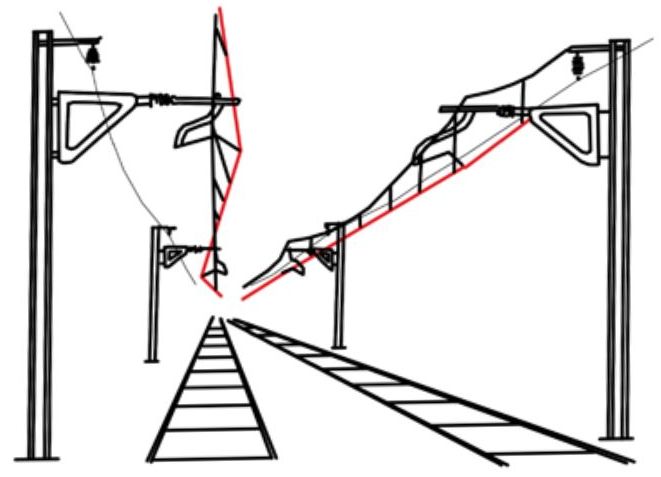My question to the young Anish Giri in 2010 was: why did the overhead contact wire that supplies power to the train we were about to take not follow a straight line? Why did it have a zig-zag pattern, as shown in this picture?
Now, after ten years and a small hint he has got it. One reader, albitex, posted the correct solution in our feedback section. I took it down and promised to switch it back on when I had published the solution. In the meantime Albitex tells me "Frederic, I am an electronic technician and I worked for a railway signalling company." Stand to reason!
And now to celebrate the New Year, nobody did a better job than Seattle's Space Needle observation tower. Do not ask me how they and do something like this. Boffins please explain!
