Winning starts with what you know
The new version 18 offers completely new possibilities for chess training and analysis: playing style analysis, search for strategic themes, access to 6 billion Lichess games, player preparation by matching Lichess games, download Chess.com games with built-in API, built-in cloud engine and much more.
Yesterday we told you how Garry Kasparov had given ten-year-old chess prodigy Vincent Keymer a study to solve, one that looked deceptively simple. After that the lad got a very subtle and instructive endgame lesson from the 13th World Champion, in form of a study which we asked you to solve.
Olge Pervakov, 4.p Moscow Sports Committee Ty Bulletin 1986
White to play and draw
After forcing Vincent to work on it in his head, in the end in fact without the pieces,
Garry sat down with the boy to analyse the study, and to explain important endgame concepts.
These are really lessons of the highest possible calibre, deeply inspiring to the chess prodigy
Vincent understood the study, and when we asked him to annotate it for us he did so without any problems. Our intention was to give you his analysis as the solution, but there was one problem: his notes were a bit difficult for normal amateurs to follow. The ten-year-old assumes that anyone can understand his evaluations, like "...leading to a draw" (but how, Vincent??). So we asked an experienced chess teacher, ChessBase editor Sagar Shah, to add some explanatory notes, for less experienced students and amateurs. If you now go through the following solution carefully you will learn quite a bit about chess endings and tempos. Don't miss it – there is no harm in adding some Elo points to your rating!
[Event "4.p Moscow Sports Committee Ty Bulletin"] [Site "?"] [Date "1986.??.??"] [Round "?"] [White "Pervakov, Oleg"] [Black "White to play and draw"] [Result "1/2-1/2"] [Annotator "Keymer,Vincent/Shah,Sagar"] [SetUp "1"] [FEN "8/k5p1/2Pb4/8/7p/4K3/3B4/8 w - - 0 1"] [PlyCount "15"] [EventDate "1986.??.??"] {It is obvious that the white king has to move towards the black g and h-pawns. But which square to choose, f2 or f3? It is impossible to decide without deep calculation.} 1. Kf2 $1 (1. Kf3 $2 {The most natural move turns out to be a mistake. Why is it you may ask? The answer is pretty simple once you have seen the main line - the white king is just one tempo too far from the g1 square.} h3 2. Bh6 {This pretty idea, which you will encounter in the main line, doesn't work here.} gxh6 $1 3. Kf2 Bh2 $1 4. Kf3 h5 $1 {[%csl Gg1,Gg2,Gg3,Gg4] and all the squares for the white king have been blocked.}) 1... h3 $1 { Black cannot allow Kg2-h3 and hence this move is sort of forced.} (1... Kb6 2. Kg2 Kxc6 3. Kh3 Be7 4. Be1 g5 5. Bd2 Kd5 6. Bxg5 $11) 2. Bh6 $3 {The key to the entire problem. This is the move that secures a draw: White has to lure the pawn to g6 in order to win it with his king in the following variations.} ( 2. Be3+ {loses:} Ka6 3. c7 Bxc7 4. Bh6 ({or} 4. Kf3 Kb5 5. Bg1 h2 6. Bxh2 Bxh2 7. Kg4 Be5 {and Black protects his g-pawn.}) 4... g6 5. Be3 Kb5 6. Kf3 Kc4 7. Bg1 Kd5 {and Black has gained a critical tempo.}) 2... g6 (2... gxh6 3. Kg1 $11 {is a standard draw. White king will keep shuffling between h1 and g1.}) 3. Be3+ $1 {An important move not giving the b6 square to the black king.} (3. Kf3 {fails. The variation is quite pretty.} Kb6 4. Be3+ Kxc6 5. Bg1 Kd5 6. Kg4 Ke4 7. Kxh3 Kf3 $1 {And there is absolutely no way to stop the march of the g-pawn followed by evicting the white bishop from the g1-a7 diagonal. You can check this for yourselves.}) 3... Ka6 4. c7 (4. Kf3 {works as well.} Kb5 5. Bg1 $1 Kxc6 (5... h2 6. Bxh2 Bxh2 7. Kg4 $11) 6. Kg4 Bc5 $1 (6... Be5 7. Kxh3 $11) 7. Bh2 $1 $11 {and it's a draw.} (7. Kxh3 $2 Bxg1 8. Kg4 Be3 $18)) 4... Bxc7 5. Kf3 Kb5 6. Bg1 h2 (6... Kc4 7. Kg4 {and White can pick up the g6 pawn in time. Of course} Bd8 8. Kxh3 {is a draw.}) 7. Bxh2 Bxh2 8. Kg4 $1 {and now the black pawn cannot be defended – since it is on g6 and not on g7!} 1/2-1/2
Now for the final problem Vincent was given during that memorable two-hour session in Berlin:
It was a delightful puzzle which everyone present in Garry's suite thoroughly enjoyed
White to play and win
Yes, White is in check, and he has just four legal moves (one of which, 1.Rf7, lead to an immediate mate with 1...Qxf7#. So which of the other three should White play? Try to work this out in your head, and remember: it is quite appropriate to grin in delight, as Vincent did, when you find the winning line.
The first mate-in-two problem published on the 26th was the following:
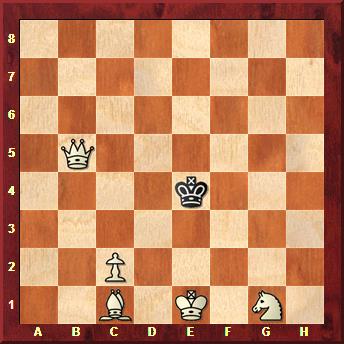
White to play and mate in two.
The next twin involves moving the knight g1 to e3:
Mate in two moves
Once again we ask our readers to solve the problem and then construct a new position by moving or inserting a single piece on a different square. The new problem must again be a mate in two, with a different solution. And it must have no "cooks" – multiple solutions that will spoil an chess problem.
