The great physicist and Nobel laureate Richard Feynman, often compared and likened physics to chess. This tendency of his could be an excellent starting point for the present analysis, if only it had not already been discussed in the following article published at ChessBase, "Feynman: Using chess to explain science". Therefore, I will simply proceed to mention some of the laws of physics that also apply to chess.
Law: Conservation of Energy
Let's begin by discussing one of the key properties in nature: Energy.
Feynman states:
…The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in the manifold changes which nature undergoes… it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.
This applies to almost nothing else around us! Among the countless things that can be measured in nature (the leaves of a tree, the speed of a car, age, height, etc.), there are only 7 that remain the same regardless of time and space, energy being one of them. Consider how important it is to find something stable in a world where everything changes! In such a world where almost all figures increase or decrease, grow or diminish, we can have something we can trust; a number that will always be the same!
The pendulum constitutes a simple example of this:
Assume a bob is placed at point A. At the moment of release it has no speed (i.e. kinetic energy), but is the recipient of two forces: the force of gravity (dark red) and the tension force of the string (green). When a body is acted upon by certain forces, these forces provide it with the potential to do something – such as move – which is why, at point A, the bob has potential energy. Naturally, the bob then moves to point B, where it is noted that the two forces neutralize each other. Therefore, it no longer has any potential energy. Was that energy lost? Certainly not! At point A, the bob was motionless, but when it was released, it started accelerating, thus turning its initial potential energy into kinetic energy!
At this point, it would be interesting to examine how the energy conservation law is also applicable in chess. The only difference in chess is that Energy is called Advantage and the law is: The transformation of advantages.
Kramnik - Aronian
However, a question inevitably arises: if energy is conserved and remains constant without ever being lost or produced but only transformed into a different form, then how was everything we see and experience around us created? How was this energy created if nothing existed in the beginning? Who raised all these impressive mountains; who created the stars and the galaxies?
One theory suggests that perhaps this energy was never created! ... Or rather, it was created, but the total energy in the universe still remains zero! In nature, positive energy is always accompanied by negative energy. For example, it is still impossible to jump to the moon! The reason for this is because, the Earth has surrounded itself with negative energy which traps us in. In physics, we call such situations as bound states.
The exact same thing happens in a game of chess! The initial energy equals zero if we were to assume White has the positive energy while Black the negative. Consequently, in order for the white player to win (increased positive energy), the black player ought to commit an error (resulting in negative energy). Otherwise, no matter how well the white player plays, he will never be able to gain an advantage and win.
As one would expect, it is impossible to discuss energy without mentioning Einstein’s famous formula E=mc2! According to this, mass equals energy multiplied by a certain number... a very big number! ... And, not only is this number big, it is even squared, which indicates that mass can produce a huge amount of energy!
The aforementioned formula also applies in chess. Of course, in chess, as in physics – where nuclear reactors are needed to create the result described above – it is crucial that mass be offered in the right way and at the right time to obtain the maximum amount of energy. This method is called “sacrifice” or “combination” and can be equally impressive and imposing as a nuclear explosion!
Sacrifice in chess is reminiscent of certain phenomena observed in nature: after something is destroyed, the bodies left around it absorb some “extra” energy provided by it.
G. Kasparov – V. Topalov
The space in which the bodies move plays a pivotal role in the theory of relativity! Let us examine the chess board within a physical framework:
Minkowski Geometry
In this picture, the white king intends to climb to the 8th line. Which route is shorter: the green or the yellow one? None! Counting the number of steps required, the two routes are the same, as, in both cases, the king will need to move seven steps ahead. It seems that in chess, the length of the side of the triangle is equal to the hypotenuse –a fact that would greatly displease Pythagoras!
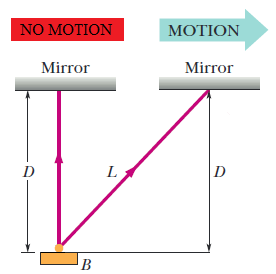
This picture here presents one of the standard charts of introduction to Minkowski geometry. Let us suppose a light beam is emitted perpendicular to the ceiling inside a moving train. On the left, this light is portrayed as observed by a passenger of the train, while, on the right, the same light beam is portrayed as observed by someone standing on the street, who sees the train passing in front of them!
It is therefore obvious that chess and relativity share numerous similarities!
One of the most bizarre and funny ideas borne by relativity was the deformation of the bodies as they approach the speed of light. The faster a body moves the thinner it appears; in other words, running is a slimming activity! The deformation of the “size” of objects also exists in chess when fast attacks start occurring!
Jorge Szmetan – G. Garcia Gonzales
Similar to the law of energy conservation, there is another law dictating the conservation of color charge; one of the most recent laws discovered! It states that quarks inside a nucleus have “color” which must be conserved! We will not go into too much detail in regard to this law. It suffices to say that it also applies in chess!
Larsen –Spassky
Let us conclude with a chess game played in Princeton many years ago, by two great physicists:
Albert Einstein – Robert Oppenheimer
Physics and chess have always been – and still remain – my two greatest loves, even if, at times, I cheat on them both! What attracts me the most is the mystery that hides underneath their veil. I hope this short analysis succeeded in showcasing a few of the reasons why they have captured my heart!
About the authorIoannis Halkias is a physicist with a wide range of academic interests, from physics and mathematics to politics and philosophy. As a kid he had shown talent and love for natural sciences and thus entered the physics department at the University of Crete where he is now working on physics and on the mathematics of finance. His hobbies mainly revolve around sports, music – and chess. He also served as a Green Beret Corporal in the Greek Special Forces. |
 |
