Winning starts with what you know
The new version 18 offers completely new possibilities for chess training and analysis: playing style analysis, search for strategic themes, access to 6 billion Lichess games, player preparation by matching Lichess games, download Chess.com games with built-in API, built-in cloud engine and much more.
Ultimately chess is just chess - not the best thing in the world
and not the worst thing in the world, but there is nothing quite like it.
– W.C. Fields
The Federal Ministry of Science and Research in Germany had proclaimed 2008 the “Year of Mathematics”. In addition, in 2008 both a Chess World Championship and a Chess Olympiade took place, so that one may also think of 2008 as the “Year of Chess”. This provides more than enough reason to look at an interesting problem at the interface of these two intellectual activities: mathematics and chess. It is a fascinating paradox which seems to prove that 64 is equal to 65 simply by cutting a chessboard (which, of course, consists of 64 squares) into four pieces and by assembling these pieces into a rectangle whose sides are made up of 5 squares and 13 squares, respectively (which, of course, results in an area of 5 . 13 = 65 squares).
Specifically, what I have in mind is this:
With three straight cuts the chessboard has been dissected into two equal triangles and two equal trapezoids. The sum of the areas of these four pieces is 64 little squares of the chessboard. These four geometric pieces of the chessboard dissection may now be reassembled into the following rectangle.
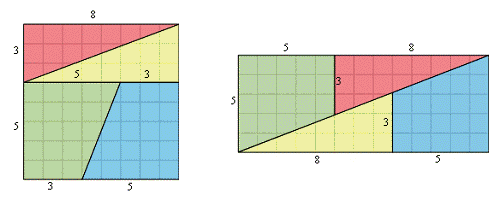
Please compare each of the four pieces in the two diagramms. The sides of the resulting rectangle are made up of 5 and (8+5) = 13 little squares. Hence the area of the rectangle is 5 x 13 = 65. These are the same four pieces as cut out from the chessboard, only arranged differently. Hence their total area must also be the same.
Therefore, we have proved that 64 = 65! Obviously, this is not true and there must be a mistake somewhere. Can you find it?
What lies at the center of the above paradox are drawing inaccuracies of the lines that make up the triangles and the trapezoids and hence the rectangle. Drawn at a higher resolution, the above diagramm should look like this:
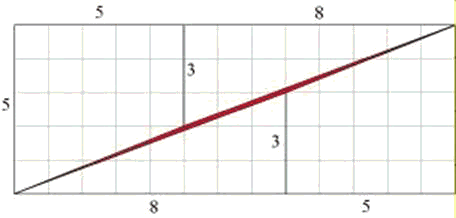
And zooming in on the central area one sees the rift between upper and lower parts even more clearly:
The area highlighted in red in the above diagramms has the shape of a very long parallelogram. It is responsible for the difference in area between the square and the rectangle.
A similar dissection paradox can be constructed when starting with a 13x13-square and rearranging the two triangles and two trapezoids that make it up into a 21x8-rectangle in a similar fashion as above:
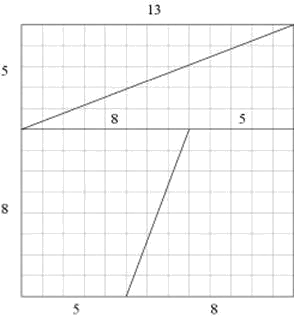
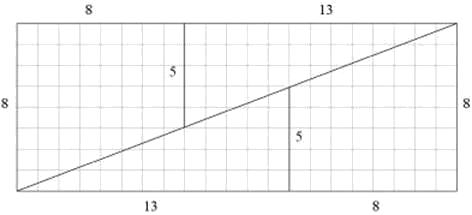
Again at a higher resolution we have:
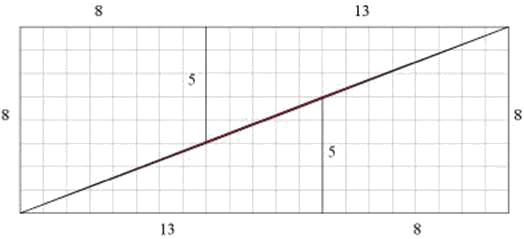
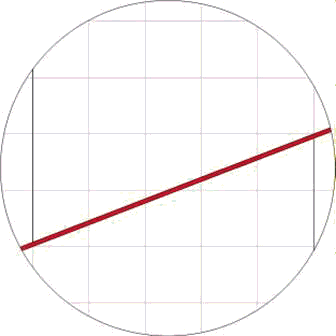
The area colored in red is again a parallelogram of area 1 where this time the upper and lower parts do overlap. Hence in this case, there is no rift here, but the resulting rectangle has a smaller area (=168) than the original square (=169) due to the overlapping.
What is the mathematical core of this paradox? To explain it in general, we start by mentioning the sequence of so called Fibonacci numbers Fn. This is a sequence of numbers in which each following number Fn+1 is defined as the sum of the two immediately preceeding numbers Fn and Fn-1. Hence:
Fn+1 = Fn + Fn-1 for all n = 1, 2, 3, …
The starting values are given by F0 = 0 and F1 = 1. Thus the first few values of the Fibonacci sequence are
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
The above dissection paradox then seems to say that
Fn . Fn equals Fn+1 . Fn-1
Let us perform some simple calculations to see what is really going on:
Fn . Fn = Fn(Fn-1 + Fn-2) = Fn . Fn-1 + Fn . Fn-2
and
Fn+1 . Fn-1 = (Fn + Fn-1)Fn-1 = Fn . Fn-1 + Fn-1 . Fn-1
The difference Dn between these two products is:
Dn = Fn+1 . Fn-1 - Fn . Fn
= Fn-1 . Fn-1 - Fn . Fn-2
= -Dn-1 = (-1)2 Dn-2 = ... = (-1)n-1D1 = (-1)n
since D1 = F2 . F0 – F1 . F1 = 1 . 0 – 1 . 1 = (-1)1.
Therefore we have established the truth of what is known as Cassini`s identity:
Fn+1 . Fn-1– Fn . Fn = (-1)n
The conclusion is: One can always reorganize an Fn x Fn -square into an Fn+1 x Fn-1 -rectangle and the difference between their areas, namely Fn . Fn and Fn+1 . Fn-1 respectively, is (-1)n , i.e. either -1 or +1. In the first case, one has an overlap between the pieces. In the second case, there is a rift between them.
The next largest square for which the dissection works is a 21x21-square which in the above fashion may be reorganized into a 34x13-rectangle. You may work out how the 21x21-square needs to be cut by simply thinking of the Fibonacci sequence.
|
Previous articles for ChessBase:
About
the author
