Winning starts with what you know
The new version 18 offers completely new possibilities for chess training and analysis: playing style analysis, search for strategic themes, access to 6 billion Lichess games, player preparation by matching Lichess games, download Chess.com games with built-in API, built-in cloud engine and much more.
Those who go beneath the surface do so at their peril. – Oscar Wilde, The Picture of Dorian Gray
I am convinced that, because of its depth and inexhaustibility, chess is capable of a continuing development, that laws are at work which have not yet been recognised, that there are paths the forks of which we can only imagine and that possibilities lie before us for which we have not yet worked out the reasons. – László Wekerle
As is the case in life itself, in chess there are uncounted basic situations which belong to the standard repertoire, such as the knight fork of king and queen, the bishop sacrifice on h7, the back-rank mate, the pin, to name but a few of them. These motifs may be found more or less obviously on the surface and thus stand out from the position, or lie as yet undiscovered at some archæological level or other. Generally speaking, the more deeply they are hidden, the harder it is to find them, because the tree of variations which results from a position usually branches out very quickly and one is faced with the phenomenon called combinatorial explosion. With an average of 40 possible moves per side and per move, if we go ten moves deep there are approximately (402)10=1.1 x 1032 different ways through the tree of variations. This chapter is devoted to the strat agem of the knight fork and shows examples of it being buried sequentially deeper in the position.
The unadulterated motif, in broad daylight: 1.Nf7+ and the black monarch and his consort are within range of the knight. 1-0.
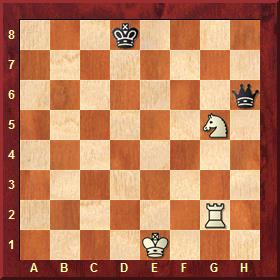
Wade-Boxall, Middleton-on-Sea 1953
Black has just offered an exchange of queens. An inappropriate offer with unpleasant consequences in the form of the loss of a piece or of mate by 1.Bxf7! Rxf7 2.Ng6+ 1-0.
Yates-Réti, New York 1924
With the nonchalant 1.Ng5! White throws his second knight into the scales and at the opposing king. The latter can do nothing but stand by and witness a bitter catastrophe: 1...Qxg5 2.Rh8+ Kxh8 3.Nxf7+. Black's position is decisively destroyed and he has lost material. He would be even worse off after 1...Rf8 2.Qg4 (with the threat 3.Rh8+) 2...f6 3.Qh4 and then mate. Réti called it a day: 1-0.
Zukertort-Englisch, London 1883
White’s c-pawn has long since left behind his role as a mere servant. It is the leading actor in a finish which is as short and succinct as the finale of a western. White is the first to draw his colt: 1.Qb5 Qxb5! c8 Kf7 Qxe6 Kxe6 and the knight fork with 4.Nc7 gives White a clearly won position: 1-0.
Anisimov-Chebotarev,
Russian Championship U20, Vladimir 2002
A setup which invites White to take violent measures against g6, and in fact 1.Bxg6 is a hammer blow. Everything, even including 1...hxg5 2.hxg5 Nd5 3.Bxf7+ Rxf7 4.Rh8+ Kxh8 5.Nxf7+ now leads to a simple victory for White: 1-0.
Schlechter-Mieses, St. Petersburg 1909
Mieses really puts his shoulder to the wheel and produces a decisive and unexpected manœuvre: 1...Bxe5 2.dxe5 Qh4 3.Rg3 Qxh2+ 4.Kf1 Rxd1+ 5.Rxd1 Qxg3 6.Nxg3 Ne3+ a procedure about which there can be no complaint, because Black is the only one who can win the endgame: 0-1. Schlechter, who shortly after drew a World Championship match against Lasker, should have tried not 3.Rg3 but 3.Qc5, with the idea of Qxa7, afterwhich Black's superiority is less oppressive and White can still perceive a flicker of hope.
Kutuzovic-Faragó, Budapest 1995
White ex ploits the chance to play 1.hxg6 hxg6 2.Qh2 Kf7 3.Nf3 Rh8 4.Ng5+ Kg8 5.Qxh8+ Bxh8 6.Rxh8+ Kxh8. Now the thematic knight fork 7.Nf7+ leads to an endgame which, when the smoke has cleared after 7...Kg7 8.Nxd8 Rxd8 9.Bxa7 was converted to the full point by White: 1-0.
And so on and so forth. Every motif can lie buried beneath the surface of a position at differing levels. The art of chess consists of discovering it there and bringing it to the light of day, like a miner or an archæologist.
Select games from the dropdown menu above the board
Note: The Joys of Chess contain an extensive seven-page list of bibliography with references to works that were used in researching its 94 essays. This list is not included here with the above sample chapter.
The Joys of Chess is an unforgettable intellectual expedition to the remotest corners of the Royal Game. En route, intriguing thought experiments, strange insights and hilarious jokes will offer vistas you have never seen before.
The beauty, the struggle, the culture, the fun, the art and the heroism of chess – you will find them all in this sparkling book that will give you many hours of intense joy.
Christian Hesse is a Harvard-trained professor of Mathematics who has taught at the University of California, Berkeley (USA), and since 1991 at the University of Stuttgart. He has written a textbook called 'Angewandte Wahrscheinlichkeitstheorie'.
Chess and literature are his main hobbies, and he also likes fitness and boxing. His heroes are the ones who fall to the bottom and rise again, fall and rise again…
From the foreword by by Ex-World Champion Vishy Anand: "A rich compendium of spectacular highlights and defining moments from chess history: fantastic moves, beautiful combinations, historical blunders, captivating stories, and all this embedded into a plentitude of quick-witted ideas and contemplations as food for thought."
