ChessBase 17 - Mega package - Edition 2024
It is the program of choice for anyone who loves the game and wants to know more about it. Start your personal success story with ChessBase and enjoy the game even more.
In chess training, the thinking aloud method may be used. On the basis of such verbal reports, a chess player or his/her trainer may build a specific decision tree, containing all the moves considered. Then, from the decision tree, nine indicators may be abstracted and measured:
These indicators can be interpreted in terms of problem-solving cognitive strategies. This article demonstrates the methodology of using nine indicators to analyse chess players' complex problem-solving processes.
It is recommended for the reader — at the beginning of the article — to solve the presented tasks himself and carefully write down his thoughts, especially the amount of variations (all the moves considered).
Garry Kasparov, a former World Champion, was once called "a monster with a thousand eyes and from another age". In the phrase, Tony Miles paid tribute to his incredible ability to calculate broadly, deeply and quickly. On the other hand, in 1907 it was Jose Raul Capablanca who said: "I see only one move ahead, but it is always the correct one". This was the answer he gave to a question about his success in chess (Ross 2006).
Master Class Vol.4: José Raúl Capablanca
He was a child prodigy and he is surrounded by legends. In his best times he was considered to be unbeatable and by many he was reckoned to be the greatest chess talent of all time: Jose Raul Capablanca, born 1888 in Havana.
Basler Zeitung, 15 May 1986, page 35
So where is the truth? Here and there. According to psychologists, there are at least two basic pillars in chess development:
The first factor is strongly related to chess knowledge; the latter with operational skills.
These two basic pillars will be shortly analysed below. The aim of the article is to present the reader a certain method for psychological chess training.
But first of all I offer the reader a chance to "think aloud" and write down all the variations in this position (Fig. 1). The value of the data obtained by the "thinking aloud" method depends largely on whether the subjects are able to freely and reliably verbalise their thoughts. Therefore, prior to proceeding with the experiments, the experimenter or trainer had to train the chess players to solve problems on the board, so that they would be able to simultaneously verbalise their process of thinking while working on the chess activity.
Compare your decision tree with the one drawn by a very strong master. His verbal comments are omitted here.
He discovers very soon the threat Rxf3 and the possibility of a sacrifice on d7:
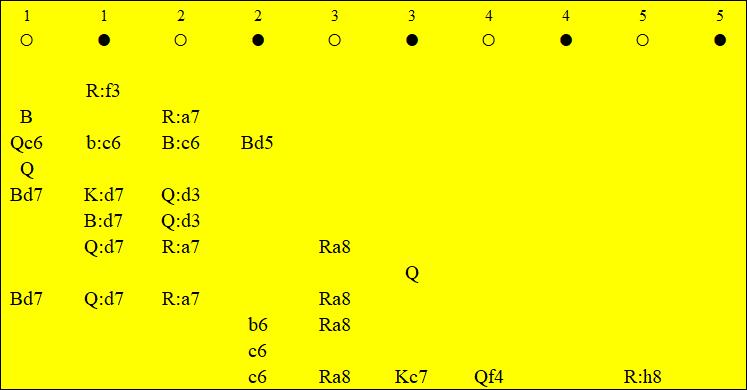
Fig.2a. Sample decision tree, considered by the subject from Fig.1
He thinks White is winning. Suddenly, the defence 2…Qd6 comes to his mind:
Fig.2b. Sample decision tree, considered by the subject from Fig.1
So he starts the process which de Groot called "progressive deepening", a very important step in calculation (Fig. 2c)!
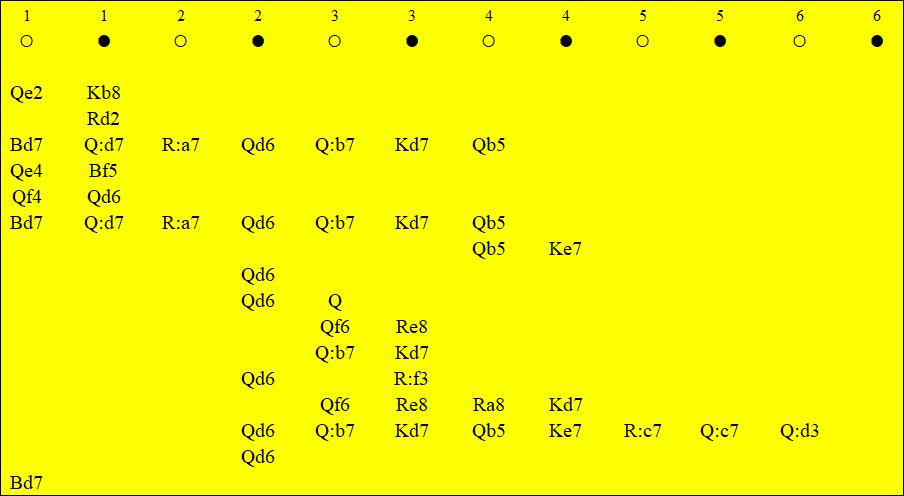
Fig.2c. Sample decision tree, considered by the subject from Fig.1
White has just discovered that 1.Bd7 Qxd7 2.Rxa7 Qd6! is losing and now is looking for other options (Fig. 2d):
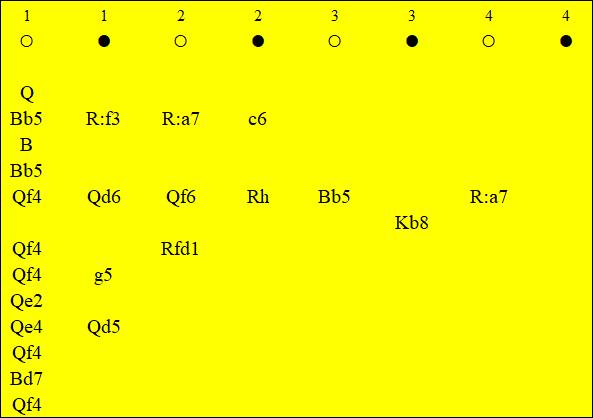
Fig.2d. Sample decision tree, considered by the subject from Fig.1
But still, the possibility of 1.Bd7 is tempting. However, he decides to play a more positional move (Fig. 2e):
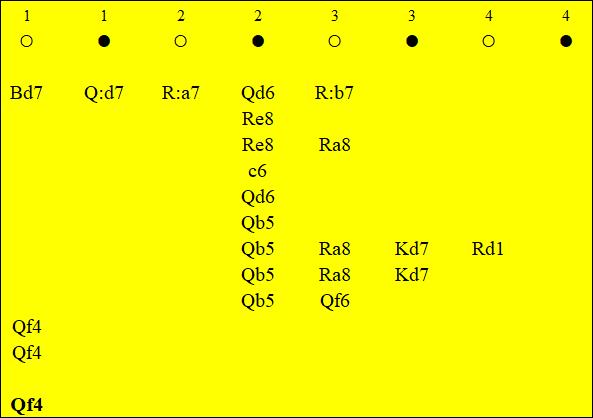
Fig.2e. Sample decision tree, considered by the subject from Fig.1
The final choice is Qf4.
Therefore, 1.Bd7 Qxd7 2.Rxa7 Qd6! 3.Qxb7 Kd7 4.Qb5 Ke7 5.Rxc7 Qxc7 6.Qxd3 leads to Black's win. White has a real choice between 1.Qe2, 1.Qe4 or 1.Qf4.
Look at the possible variations and compare with your verbal protocol:
You play 20 moves of elegant positional chess - but throw the game away by miscalculating. To play a good game of chess you must know how to calculate. The ability to calculate is not something that chessplayers are born with. Calculation is a core skill that can be improved through practice. In this 10th Power Play DVD Grandmaster Daniel King will help you to assess how good you are at calculating, and gives you tips as to how you might sharpen your thought processes at the chessboard.
Of course, you may also use the following popular position, used by Adriaan de Groot. Then you will have the possibility to compare your thinking with verbal protocols by Alexander Alekhine, Max Euwe, Paul Keres, Savielly Tartakower, Reuben Fine… (de Groot, 1965; Fig. 3).
Look at the possible variations and compare with your verbal protocol:
So you have collected one or two protocols of your thinking. It is time to analyse them according to the Nine Indicators method.
In the field related to the methodology of chess psychology, the classic work of the Dutch researcher Adriaan de Groot still plays a leading role (de Groot 1965, 1981). The idea presented in this article refers to his concept, mainly as it is based on a "thinking aloud" method. I have been developing a method for broadening and deepening of thinking processes for years, by controlling the nine important indicators (see Przewoznik 2003, and Przewoznik, Soszynski 2001).
Let us imagine the thinking process in a very popular study by Richard Reti (Fig. 4).
Of course, in all the examples the reader can analyse himself and save the solution first.
This may be presented as a process of some kind of "ideal" thinking. Look at the decision tree below (Fig. 5).
Fig. 5. Reti's study - the decision tree
Several quantitative indicators of individual ways of solving problems on the chessboard can be determined, namely: M, N, A, Dmax, nn, Pmax, Pser, T, W. These indicators were introduced by Adriaan de Groot (1965), in order to analyse "thinking aloud" protocols. In this article, only the names of indicators are modified, visualised and adapted to computerised statistical programs. These indicators give a wide range of opportunities for the study of thinking (Przewoznik & Soszynski 2001, Przewoznik 2003).
First of all, you may pay attention to the indicators in the decision tree, and then train them separately. When you decide what to do in a critical position and train your thinking, you may also ask yourself some adequate training questions. Examples are recorded below.
M - denotes the number of all considered moves contained in the entire decision tree. This can be used to measure moves in chess and also to analyse other decision-making situations. This indicator allows us to distinguish between those individuals who seek more information for decision making and those who make decisions on the basis of a smaller amount of information.
Possible questions:
I often choose positions like the following, where the subjects have to calculate many and long variations if they want to find a solution. A fantastic example is the game played by my club friend Michal Krasenkow (Fig. 6).
Solution: 20.Rd3!! White had to check:
Always winning.
The whole game is worth your consideration, as it included many strange and surprising moves:
N - denotes the total number of subsequent proposals to solve. This number may be a reflection of the subject's mentality type. A large value of N would be consistent with an empirical mentality type — a chess player who prefers a problem-solving approach based on the processing of large amounts of data and the calculation and verification of a large number of multiple variants. In contrast, a relatively smaller value of N may be characteristic of the theoretical chess player type, whose thinking is less empirical and more deductive, without specific variants. On the other hand, the value of N may be a function of the position on the chessboard, where the more complex a position is the greater the value of N, as more variations need to be calculated.
Possible questions:
I often choose positions where the subjects have to count many but not too long variations if they want to find a solution (Fig. 7).
The whole game was used in the Soviet Union as a test to check the following skills: sense of the position, calculation of variations, originality, resourcefulness, sudden change in pawn formation, discipline of thought and the need to compare options (Zlotnik 1990).
Solution: Black had to calculate:
19…Qxc6 20.e5 Qc5+ 21.Kh1 with a lot of subvariations:
19…Bxa1 with a lot of subvariations.
19…Bxe5
A - denotes the set of alternative actions (candidate moves) considered by the subject, here understood as equal to the set of options in the decision-making process. In our example A = 6, since in the formula there appear six different solving propositions, a, b, c, f, g, h. Repetitions are omitted. The value of A may have a definitive psychological content: it can be associated with the fluency and semantic versatility of spontaneous thought (Guilford 1967). It can be assumed that persons characterized by great fluency and versatility would consider many different solving propositions in the process of choosing moves. It may be that fluency of thought will be more closely correlated with the value of N, whereas versatility more closely with the value of A. As in the case of N, the value of A may depend on the situation on the board and not only on the individual traits of the chess player.
Possible questions:
Sometimes I choose positions so that the respondents have to look for a few options (called in Russia or the Soviet Union "moves-candidates") before they can come up with the right idea. The amount of possibilities must be small. I choose research models with three to seven options. Sometimes participants surprised me by offering new options (Fig. 8).
Solution: Samuel Lloyd gives the incredible variations starting with 1.Ke2! Brave the King!
1.Ke2 f1=Q+ (1...Kxe4 2. Bd3+ Kd4 3. Rf4#; 1... cxd2 2.Rxf2+ Kxe4 3.Bd3#; 1... axb5 2.Rxf2+Kxe4 3. d3#) (1... Nc1+ 2. Ke3 f1=Q 3. Rxf1#) 2. Ke3.
One day in Miedzyzdroje, Izabela Siekanska (a master) discovered 1. Bd3+ Kd4 2. Rf3+ e5 (2... Be5 3. Bxe5#) 3. Rd5 mate!
The other six indicators and the explanation of "The Chunking Theory" will be published in Part 2 to follow shortly...
