Winning starts with what you know
The new version 18 offers completely new possibilities for chess training and analysis: playing style analysis, search for strategic themes, access to 6 billion Lichess games, player preparation by matching Lichess games, download Chess.com games with built-in API, built-in cloud engine and much more.
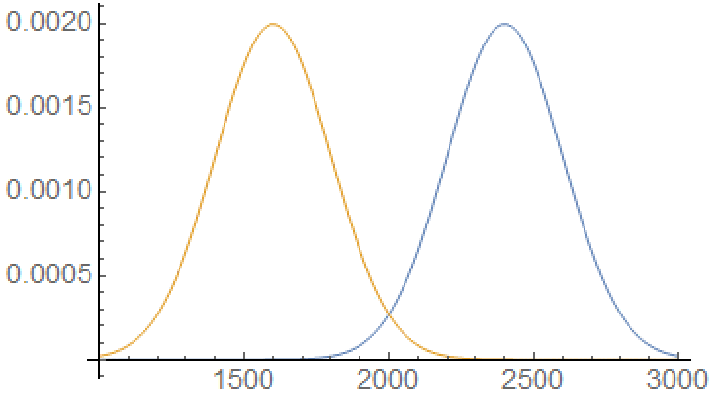
Performance ratings struggle to deal with perfect scores. Some online calculators will simply add 400 points if you win all your games, but that is incorrect. The performance rating should be infinite. To see why, we have to understand how the Elo ratings work. In a game between a 1600 and a 2400, there is a normal distribution centered at 1600 and another centered at 2400. Of course, the 2400 is the heavily favored to win. However, there is still some overlap in the graph, which means that there is a small chance of an upset. Thus, even a 2400 would not be expected to get a perfect score against 1600s; someone who achieves that would have a performance rating above 2400. Only a player with an infinite rating would be expected to win all their games.
So perfect score = infinite performance rating. However, this leads to unrealistic results. That amateur tournament where I went 3.0/3 isn’t better than Caruana’s 2014 Sinquefield Cup. A perfect score against amateurs is less impressive than a plus score against super GMs, and I developed MinStrength to reflect that.
A performance rating asks, "Who would be expected to score as well as you did?" Caruana’s performance rating was 3100 at the 2014 Sinquefield Cup. For any human, that is extraordinary, but for a 3100 player, it would just be an average tournament. They would not gain any rating points.
MinStrength asks, "Who would not be expected to score as well as you did?" Consider a 1500 player. Sometimes they have a bad tournament and play like a 1300. But there are other times when they perform at the 1700 level. But even in their best tournament ever, they don’t perform at the 2700 level and earn a GM norm. That is outside of their range. How low would your rating have to be for a result to be outside of your range? That is your minimum strength, or MinStrength.
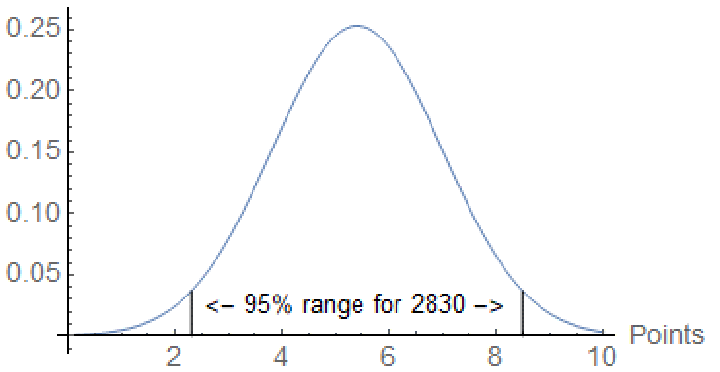
Let’s go back to the 2014 Sinquefield Cup. A 2830 would have an expected score of 5.4/10. With some math (methodology: http://e4stat.blogspot.com/2023/03/minstrength-methodology.html), we can calculate the range. 95% of the time, a 2830 should score between 2.3/10 and 8.5/10. Caruana was at the upper end of that range, so his MinStrength was 2830.
MinStrength has several desirable features. Perfect scores result in an infinite performance rating, but not an infinite MinStrength. According to MinStrength, scoring 3.0/3 against amateurs is much less impressive than Caruana’s 2014 Sinquefield Cup. MinStrength also rewards consistency. For example, consider the Candidates match between Fischer and Larsen (2660). Suppose that after winning Game 1, Fischer got into a dispute with the organizers and quit. His performance rating would still be infinite whether he scored 1.0/1 or 6.0/6. But 1.0/1 against a 2660 would be a footnote in chess history; 6.0/6 is legendary. Fischer’s MinStrength was 2426 after winning Game 1. It rose to 2737 after Game 6. If we combine it with his 6.0/6 against Taimanov (2620), Fischer’s MinStrength is 2838.
If you want to find your MinStrength, check out the calculator on my website. Here are the results for some selected tournaments. Rating inflation may affect the results. However, Ken Regan argues that there has been no rating inflation. Using chess engines, he and his co-author show that 2500s in the 1970s played about as accurately as 2500s in the early 2000s. Their results were similar for other ratings. If there is no rating inflation, then historical MinStrengths can be compared with modern ones.
1. Caruana, 2014 Sinquefield Cup. The highest MinStrength of all time: 2830. Caruana scored 8.5/10 and his average opponent was rated 2802.
2. Carlsen, 2009 Nanjing. He scored 8.0/10 and his average opponent was 2762. MinStrength = 2755.
3. Fischer-Larsen, 1971 Candidates Match. Fischer won 6-0 against a 2660. His MinStrength was 2737.
4. Karpov, 1994 Linares. His 11.0/13 is very impressive, but his average opponent was rated 2682, which is lower than in modern super tournaments. His MinStrength was 2736.
5. Topalov, 2005 San Luis. He had a terrific start, scoring 6.5/7 in the first half. Then he made 7 draws to clinch the World Championship. Overall, his 10.0/14 against 2731-rated opposition leads to a MinStrength of 2699.
6. Fischer-Taimanov, 1971 Candidates Match. Fischer won 6-0 against a 2620. His MinStrength was 2697.
7. Kasparov, 1997 Linares. He scored 8.5/11 and his average opponent was 2693, so his MinStrength was 2668.
...
The Author, That Amateur Tournament Where He Went 3.0/3. Though my performance rating was infinite, this result is not in the same league as the others. My average opponent was 1796 FIDE, and my MinStrength was 1753.
References
Regan, Kenneth Wingate, and Guy McCrossan Haworth. "Intrinsic Chess Ratings." In Twenty-fifth AAAI Conference on Artificial Intelligence. 2011.
Methodology [Published on my blog]
In a game between Players A and B, there is a normal distribution centered at A’s rating and another centered at B’s rating. The standard deviation is 200. In the Elo system, the expected score for Player A is the probability that a random number from A’s distribution is higher than a random number from B’s. This seems to ignore the possibility of draws – there is a 0% chance that both random numbers are equal – but that will be addressed later. The expected score can be approximated with the logistic function:
Next, I model a tournament as n games against your average opponent. This is an approximation (the expected score isn’t a linear function, so a game against an 1800 followed by a game against a 2000 is slightly different from playing two games against a 1900). With this assumption, your score follows a binomial distribution. The mean is np and the variance is np(1-p), where p is your expected score against the average opponent. The issue with this binomial distribution is that there is no accounting for draws. However, the binomial distribution converges to a normal distribution, so I use that as an approximation. The normal distribution is continuous, so scores such as 8.5 are possible. This means that we aren’t ignoring draws.
If you pull a random number from a normal distribution, there is a 95% chance that it will be within 1.96 standard deviations from the mean (np). The standard deviation is the square root of the variance, so that will be (np(1-p))1/2. Thus, the upper end of the 95% range is np + 1.96(np(1-p))1/2. Therefore, your MinStrength is the rating such that score = np + 1.96(np(1-p))1/2
