Do Chess Players and Scientists Need Intelligence?

Chess is an old war game. Two people battle it out on a standardized battlefield, the chess board. The better one wins. Emanuel Lasker praised the "principle of justice" in chess (Lasker 1925/2010). "There is no need for incessant networking and tireless self-promotion", to make it to the top (Howard, 2009). Chess is a science that has attracted the interest of other scientists. Due to the wealth of data recorded in large databases and the reliable rating system named after its inventor Arpad E. Elo (Elo, 1978/2008), it is an important domain in the area of expertise research, a subfield of cognitive psychology. Chess players are rated on a continuous scale ranging from about 1,000 Elo points for beginners to about 2,850 points for the currently best player, Magnus Carlsen. Average club players have around 1,600 points. Players above 2,000 points are usually called experts. Grandmasters are rated at 2,500 points or higher. Winning, losing or drawing a tournament game wins or loses Elo points depending on the opponents’ rating.

On July 2, 2019, the Editorial Board of the Proceedings of the National Academy of Sciences of the United States of America (PNAS) accepted an article titled "The joint influence of intelligence and practice on skill development throughout the life span", which was authored by Vaci, Edelsbrunner, Stern, Neubauer, Bilalić & Grabner.  They had tracked 90 chess players from Austria in a longitudinal study. It focused my attention, because I was familiar with some of the scientific studies of the two authors who had partly designed research, analyzed data and written the paper, Nemanja Vaci and his doctoral advisor Merim Bilalić. It all began in December 2015. They had coauthored the article titled "Is Age Really Cruel to Experts? Compensatory Effects of Activity" (Vaci, Gula & Bilalić, 2015), which was published in Psychology and Aging, a peer-reviewed journal issued by the renowned American Psychological Association. I was stunned when I saw the curves in their Fig. 5 B. They had used the cubic function to capture the development of chess skill across the life span. It is well-known that all cubic functions are rotationally symmetric, but their curves were not. It was not clear how they had fabricated them. The late cubic rise was lacking. It was not the only error in this paper. I submitted a comment to Psychology and Aging in 2016, and a detailed revision later on. After one year of analyzing, writing, and a long time of waiting, the editor-in-chief told me:

"The short story is that I believe your critique is valid, but that the presentation of your arguments remains far too complicated and difficult to follow". He invited another major revision. I declined and told him it would be too arduous for both sides to proceed in this way, and that he should inform the Psychology and Aging readership in his own words, what he never did. The authors were employees of the Alpen-Adria University in Klagenfurt at that time, and so I asked the Austrian Agency for Research Integrity (OeAWI) to assess this case. All the Austrian universities are ordinary members of the OeAWI. The responsible member of the OeAWI Scientific Commission asked two external experts for their opinion. He did not disclose their names. He told me the experts had argued that the curves were obviously wrong, but there was no evidence of a deliberate misrepresentation. My results were published on ChessBase News, and titled "Researching age-related decline" (Wiesend, 2020).

Another paper attracted my attention. There is an ongoing controversy about gender differences in chess skill. The best male chess players are significantly stronger than the best female players. The most popular explanation is the ‘participation rate hypothesis’ by Bilalić, Smallbone, McLeod & Gobet (2009). Their article was published in the prestigious Proceedings of the Royal Society B. They found that 96 % of the difference could be attributed to the simple fact that more males are playing chess than females. Bilalić et al.’s (2009) study met with broad acceptance not only in the chess scene, but also in newspapers, magazines and the social media. It helped Bilalić win the Karpow-Schachakademie science award in 2009. People are obviously most delighted when renowned scientists confirm what they have always known. I had a closer look at this study, and found that Bilalić et al.’s (2009) argumentation was a case of circular reasoning. What should have been their outcome was actually their premise. Moreover, they had used a flawed approximation method to calculate the expected and real differences in rating. Only in this way, they could achieve their 96 % - result. My findings were published on ChessBase News, and commented by the physicist and philosopher Vera Spillner (Spillner/Wiesend, 2019).

The Benefits of Networking

PNAS is one of the most prestigious scientific journals. It is named in one breath with Nature and Science. It received more than 17,000 direct submissions in 2020. The acceptance rate was only 14 %. PNAS can afford to pick from "the world's highest-quality and most significant research", and to charge authors or their funders a publication fee of $ 2,575 for a "regular research article", and a surcharge of at least $ 2,400 to make it immediately and freely available through its open access option (PNAS Author Center). Publishing in PNAS is a privilege reserved for the top-tier scientists in the world.

Vaci et al.’s (2019) article was something special indeed. They claimed to have shown that "more able people benefit more from the same amount of learning activity". They contradicted Ericsson’s "extreme environmentalist view" who had denied the importance of innate talent, and postulated that it only takes "deliberate practice" – defined as effortful, not enjoyable practice alone, e.g. studying books – to achieve even world-class performances (Ericsson, Krampe and Tesch-Römer, 1993). K. Anders Ericsson was one of the most productive and influential, but also most criticized expertise researchers. His fiercest opponent was David Zachary Hambrick. Ericsson and Hambrick accused each other of working incorrectly (Hambrick, Macnamara & Oswald, 2020). Their dispute was fought out in a series of responses and rebuttals. Ericsson’s last response was published online in Psychological Research on June 24, 2020 (Ericsson, 2021), one week after he had died at the age of 72. The New York Times journalist Steven Kurutz wrote a well-researched obituary in which he named Hambrick as Ericsson’s critic (Kurutz, 2020).

Hambrick’s point of view is in line with Vaci et al.’s (2019) argumentation. I was surprised when I realized that he had edited their paper. Hambrick was a guest editor invited by the PNAS Editorial Board. The authors declared no conflict of interest. A Google search revealed, however, the following connections. The list does not claim completeness.

• Hambrick and Bilalić coauthored the article titled "Psychological Perspectives on Expertise" which was published in Frontiers in Psychology (Campitelli, Connors, Bilalić & Hambrick, 2015). According to the PNAS Editorial and Journal Policies "a competing interest due to a personal association arises if you are asked to serve as editor or reviewer of a manuscript whose authors include a person with whom you had an association, such as a thesis advisor (or advisee), postdoctoral mentor (or mentee), or coauthor of a paper, within the last 48 months." Vaci et al.’s (2019) paper was received for review on November 6, 2018.

• Bilalić & Vaci coauthored a chapter in The Science of Expertise, a book edited by Hambrick, Campitelli & Macnamara in 2017.

• Hambrick wrote a review about The Neuroscience of Expertise, a book edited by Bilalić. He praised it as "the first comprehensive treatment of this area of research".

• Hambrick edited the article titled "Restricting Range Restricts Conclusions" which was authored by Vaci, Gula & Bilalić and published in Frontiers in Psychology (Vaci et al., 2014). It was reviewed by Fred Oswald and Fernand Gobet. Gobet and Oswald coauthored a lot of publications with Hambrick. Gobet is Bilalić’s and Campitelli’s doctoral advisor.

• Hambrick and Campitelli are editors-in-chief and cofounders of The journal of Expertise. Roland H. Grabner, who shared senior authorship with Bilalić in Vaci et al. (2019), is one of its consulting editors. Gobet is one of its associate editors.

According to the PNAS policies, Hambrick should have declined to edit Vaci et al.’s (2019) paper. The PNAS Editorial Board should not have invited Hambrick as a guest editor.

A Longitudinal Study that was Based on a Sampling Bias

Grabner, Stern & Neubauer (2007) had screened 90 chess players from Austria with tests on figural, numerical, verbal and general intelligence. IQ (intelligence quotient) tests are widely used in expertise research as a proxy measure for innate or acquired cognitive abilities. They found that higher playing strength was primarily associated with higher scores in numerical intelligence. Vaci et al. (2019) collected all the players’ Elo ratings and number of tournament games played per year – as a proxy for all kinds of practice (!) – who had participated in Grabner et al.’s (2007) study. While ratings and games were recorded from 1994 to 2016 in a 6-monthly-rhythm, the IQ tests were performed only once in the years 2003 and 2004. Vaci et al. (2019) suggested that the IQ scores would remain constant over the entire observation period of 22 years. This assumption must be doubted. Grabner et al. (2007) tested fluid intelligence (Gf). The Cattell-Horn-Caroll theory states that Gf represents the biological, inherited part of general intelligence – e.g. processing speed or working memory capacity –, whereas crystallized intelligence (Gc) is knowledge based, and acquired through education and experience. Gf shows a peak in early adulthood before it steadily decreases, due to the influence of aging on functional neurobiological processes. Gc, instead, increases or remains stable until about the age of 70, when it also starts to decline (McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002). In other words, intelligence is a variable, whereas Vaci et al. (2019) used it as a constant. They achieved the feat to accomplish a longitudinal study based on one single observation.

Campitelli & Gobet (2011) referred to Grabner et al.’s (2007) study as "the only one that found a significant correlation between chess skill and general cognitive abilities". Ericsson (2014) assumed instead that "a selective engagement by highly respected chess players with higher IQ scores might have contributed to the observed significant correlation", because Grabner et al. (2007) had recruited their participants "through announcements at Austrian chess clubs and local tournaments, offering the opportunity to obtain information about their intelligence and personality profiles".

Figure 1 A is a reproduction of Grabner et al.’s (2007) Fig. 1, right upper panel. I used the online tool WebplotDigitizer (Ankit Rohatgi, 2019) to extract the raw data on which Vaci et al. (2019) had based their study. The number of participants was 89 instead of 90.

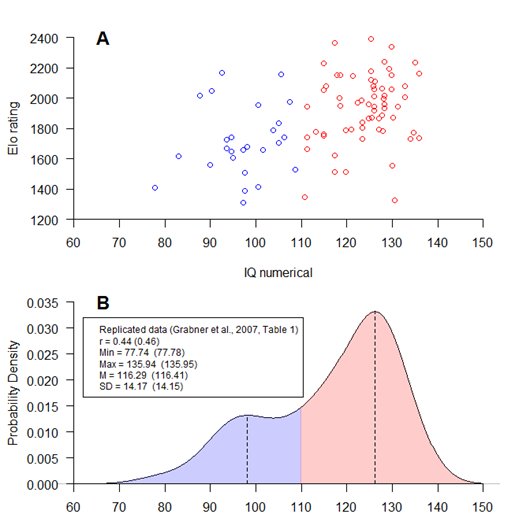
Figure 1. A: Reproduction of Grabner et al. (2007), Fig. 1, right upper panel. B: Probability density curve of the numerical intelligence scores. r, correlation coefficient; M, mean; SD,standard deviation.

The legend box in Figure 1 B shows that the replicated data excellently matched with the original ones. It is remarkable that players with extremely high numerical IQ scores of 130 or more showed such a wide range of Elo ratings, from far below-average to master level (Figure 1 A). The Shapiro-Wilk test revealed that the IQ scores were not normally distributed. The probability density curve confirmed a bimodal distribution with two maxima at IQ 98 and 126 (Figure 1 B). Grabner et al. (2007) had obviously recruited two different groups of participants: A small one with an average numerical IQ score and a big one with a score far above-average. In other words, Grabner et al.’s (2007) "clear-cut moderate relationship" between numerical intelligence and the Elo rating, which served Vaci et al. (2019) as their starting point, was an artifact resulting from a sampling bias due to ‘self-selection’. Ericsson’s guess was right.

Natural chess talent is not measurable by means of IQ tests. Bilalić, McLeod & Gobet (2007) tested an elite subsample of 23 children and found that "intelligence was not a significant factor in chess skill, and that, if anything, it tended to correlate negatively with chess skill".

Violating the Independence Assumption

Vaci et al. (2019) declined to share the raw data publicly, "in order to protect the privacy of individuals involved in the study". They contradicted themselves when they mentioned that "all participants gave written informed consent that their data can be used for research purposes and be published in anonymous form".

I drew a random sample of 90 chess players from the German database that Vaci & Bilalić (2017) had offered for download. All of them had been active for 15 years or longer. Their ratings were averaged per year and the sum of tournament games played per year was calculated. The German database does not record IQ scores, but this is not necessary to demonstrate the cardinal error in Vaci et al.’s (2019) model. Figure 2 – which is equivalent to Vaci et al’s. (2019), Fig. 1 – presents the raw data. The descriptive data in the right part of both figures show that the random sample was comparable to the authors’ original sample.

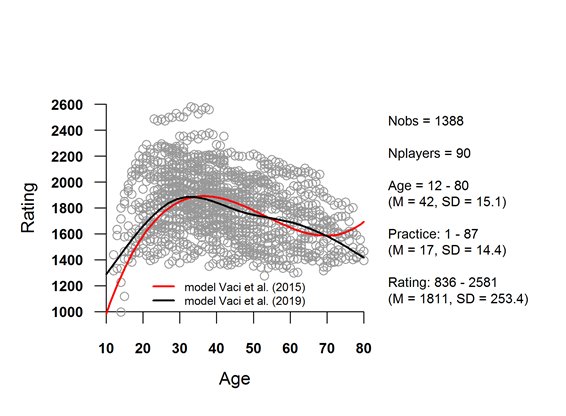
Figure 2. Raw data and fitted curves of a random sample of 90 chess players. Abbreviations of the descriptive statistics as given in Vaci et al. (2019), Fig. 1. Nobs, number of observations; Practice, tournament games played per year.

The correlation between an independent variable – also called fixed effect – like age and a dependent variable like the Elo rating can be visualized by curve fitting. In regression analysis, defined mathematical functions are used for fitting straight lines or curves to data sets by the ‘method of least squares’. Such correlations are often complex. One single function is not enough to capture them. Vaci et al. (2015) used the cubic function. The red curve in Figure 2 was obtained by their model. Cubic functions are obviously inappropriate for chess curves. Chess players do not show a ‘swan-song phenomenon’ at old age. Generalized additive modeling (GAM) is an advancement of the classical one-function method. It uses ‘smoothing splines’, which are calculated in a complex mathematical operation as the sum of weighted ‘basis functions’. The result is a line that follows the trend of the data, no matter how nonlinear or curvy it is. The black line in Figure 2 was obtained by Vaci et al.’s (2019) GAM model.

A basic principle in regression analysis – that applies to the classical approach as well as to GAM – is the ‘independence assumption’. Multiple observations per individual– Vaci et al’s. (2019) participants had about 20 observations on average – are not independent but correlated, because every chess player has her or his individual skill level. It is therefore necessary to treat each player as a separate unit, and to calculate individual curves in a first step. This is done by using random effects. Overall curves are the mean values of all the individual curves at any time point or age. Classical models that include random effects are termed ‘linear mixed effects’ (LME), while GAM is extended to GAMM (generalized additive mixed modeling). The term ‘mixed’ stands for the combination of fixed and random effects.

Bodo Winter wrote in his tutorial on LME modeling: "When you violate the independence assumption, all hell breaks loose" (Winter, 2013), and all hell broke loose in Vaci et al. (2019). They used the open source programming language R (R core team, 2021) and ‘tensor modeling’ in GAM, which is implemented in the R package mgcv (Wood, 2017), to assess the influence of the fixed effects age, number of games played, numerical IQ score and their interactions on the dependent variable Elo rating. They adhered in principle to the R code that Jacolien van Rij had published in one of her tutorials (van Rij, 2015a). The difference was that van Rij included random effects, while Vaci et al. (2019) did not. Vaci should have known van Rij’s tutorials, because he coauthored a book chapter with her on the same issue (van Rij, Vaci, Wurm & Feldman, 2018). Vaci et al. (2019) used her package itsadug (van Rij, Wieling, Baayen & van Rijn, 2017) at least to plot all their figures.

I used Vaci et al.’s (2019) model to analyze the random sample of 90 players (Figure 3 A). In a second run (Figure 3 B), ‘random smooths’ were added to their R code, according to van Rij (2015a and b).

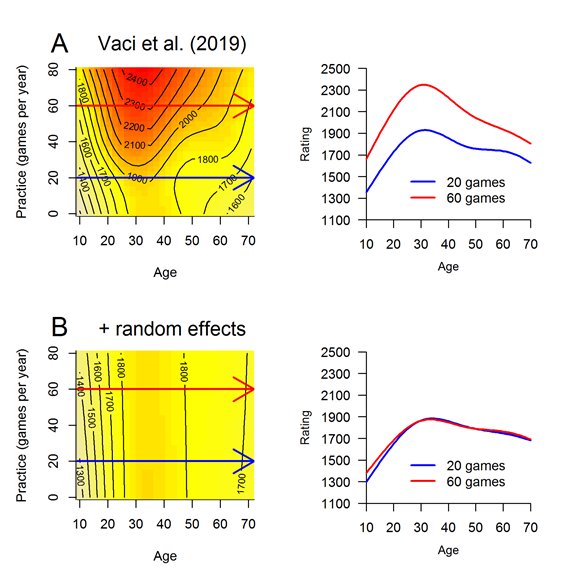
Figure 3. A: The random sample of 90 players was analyzed using Vaci et al.’s (2019) R code, and B: in a second run after adding ‘random smooths’.

Tensor models visualize nonlinear interactions as ‘surface plots’ (Figure 3, left panels). The third dimension – in addition to age and practice – is given by the color palette, with brighter colors representing lower rating scores and darker colors higher ones. The arrows in the left panels indicate which smooths are plotted in the right ones. The similarity between Figure 3 A, left panel, and Vaci et al.’s (2019), Fig. 3 B, left panel, is obvious. The rating increased significantly when 60 instead of 20 games were played per year. After adding random effects, however, playing more or fewer games had a moderate effect on the playing strength in childhood and adolescence – in periods where the rating is rising anyway –, but none in adulthood and old age (Figure 3 B). The black contour lines of constant rating scores are nearly vertical in this case.

How can one interpret these results? First, stronger players are more active in tournament chess (Figure 3 A). The stronger they are the more they enjoy doing what they are good at, and in which they are successful. Second, tournament practice does not significantly influence the individual playing strength (Figure 3 B). If stronger players were to play the same number of games as weaker players, their ratings would still be higher (Spillner/Wiesend, 2019). There must be an other causal factor instead of tournament practice. Ericsson would call it ‘deliberate practice’, while others would talk of ‘talent’. Talent and deliberate practice are synonyms in a sense. It takes talent to practice deliberately. ‘Nature and nurture’ are hopelessly intertwined. Even IQ tests are susceptible to practice effects. A "billion dollar industry" has emerged that promises their clients an improvement in psychometric tests, which are often used for classifying job applicants (Hayes, Petrov & Sederberg, 2015). The Institute of Psychometric Coaching in Australia, for example, claims that "the numerical reasoning test is the part of the psychometric testing in which you can gain the biggest improvement within a short time." Expertise researchers are confronted with the dilemma of having to separate what is not separable. They cross the boundary to pseudoscience, when their claims are not falsifiable, as illustrated by the unresolved dispute between Ericsson and Hambrick. One can always argue in hindsight that the quality of practice did not meet the criteria of ‘deliberate practice’.

Vaci et al. (2019) postulated a causal relationship between tournament practice, numerical intelligence and the playing strength that turned out to be illusory. One of the central tenets in statistics is that ‘correlation does not imply causation’. They found that adding interactions of age, practice and numerical intelligence to their model improved the "deviance explained" from 10.7 % to 47.0 % (Vaci et al., 2019, Table 1). They suggested that personality traits or the age at which the participants joined a chess club would account for the residual 53 %. They did not know that ‘deviance explained’ is a measure of ‘goodness of fit’. It quantifies the agreement between real and fitted Elo ratings. A value of 100 % means a perfect fit. The deviance explained jumped from 33 % in Figure 3 A to 99 % in Figure 3 B when ‘random smooths’ were added to their R code. Their poor deviance explained of only 47 % is the evidence of their analytical failure. Vaci et al. (2019) shared only the pleasant part of the information, but did not mention the unpleasant one.

Appendix

I submitted a manuscript to PNAS, where I explained in detail why and how Vaci et al.’s (2019) article is misinforming its readership. I managed to pass it through the PNAS Submission System after some initial difficulties. When the software asked me for my affiliations I entered "independent scientist". When it requested me to suggest three reviewers, I randomly chose three authors who had been active in this field. Authors usually suggest their friends who belong to the same academic family tree or coauthored with them in other publications, as illustrated by Vaci et al. (2014). Journals usually do not disclose their names.

The PNAS editor-in-chief informed me one week later, that the Editorial Board had rejected my manuscript, because "the likelihood that detailed review will lead to publication is low". PNAS is a member of the Committee On Publication Ethics (COPE). I asked COPE to assess this case, and raised concerns about personal associations between editor and authors. COPE has over 12,000 members – academic journals and their editors – from all areas of science (Wikipedia). It is the leading ethics institution in the academic world. The membership in COPE serves scientific journals as a certificate of their commitment to the highest ethical standards. COPE asked PNAS for a statement. The PNAS Editorial Ethics Manager provided a summary report, in which she argued that "the scientific issues with the article were reviewed by two expert members of the PNAS Editorial Board, who found no clear indication of misconduct". She stated furthermore that they had asked the authors about the situation, who had again denied any competing interests. PNAS determined "no updates to the paper were necessary". COPE told me that "upon consideration of the concerns and the member’s response, the Facilitation & Integrity subcommittee concluded that the journal followed an adequate process to handle the concerns raised about the publication".

References

Ankit Rohatgi, WebPlotDigitizer Version: 4.2, April, 2019. https://automeris.io/WebPlotDigitizer

Bilalić, M. (2017). The Neuroscience of Expertise, Cambridge University Press.

Bilalić, M., McLeod, P., & Gobet, F. (2007). Does chess need intelligence? - A study with young chess players. Intelligence, 35(5), 457–470

Bilalic, M., Smallbone, K., McLeod, P., & Gobet, F. (2009). Why are (the best) women so good at chess? Participation rates and gender differences in intellectual domains. Proceedings Biological Sciences, 276, 1161-1165.

Campitelli, G., Connors, M. H., Bilalić, M., & Hambrick, D. Z. (2015). Psychological perspectives on expertise. Frontiers in psychology, 6, 258.

Campitelli, G., Gobet, F. (2011). Deliberate Practice: Necessary But Not Sufficient. Current directions in psychological science 20 (5), 280-285.

Elo, A. E. (2008). The Rating of Chessplayers, Past & Present. Bronx, NY: Ishi Press International. (originally published in 1978)

Ericsson, K. A., Krampe R. T., Tesch-Roemer, C. (1993). The role of deliberate practice in the acquisition of expert performance. Psychol. Rev. 100, 363–406.

Ericsson, K. A. (2021). Given that the detailed original criteria for deliberate practice have not changed, could the understanding of this complex concept have improved over time? A response to Macnamara and Hambrick (2020). Psychological Research 85:1114–1120

Ericsson, K. A. (2014). Why expert performance is special and cannot be extrapolated from studies of performance in the general population: A response to criticisms. Intelligence, 45, 81-103.

Grabner, R. H., Stern, E., Neubauer A. C. (2007). Individual differences in chess expertise: A psychometric investigation. Acta Psychol. (Amst.) 124, 398–420.

Hambrick, D.Z., Macnamara, B. N. & Oswald, F.L, (2020). Is the Deliberate Practice View Defensible? A Review of Evidence and Discussion of Issues. Frontiers in Psychology 2020; 11: 1134.

Hambrick, D.Z., Campitelli, G., Macnamara, B.N., (2017). The Science of Expertise: Behavioral, Neural, and Genetic Approaches to Complex Skill, New York, NY: Routledge.

Hayes, T. R., Petrov, A. A. , and Sederberg, P. B. (2015). Do We Really Become Smarter When Our Fluid-Intelligence Test Scores Improve? Intelligence. 48: 1–14.

Howard, R.W. (2009). Individual differences in expertise development over decades in a complex intellectual domain. Memory & Cognition 37 (2), 194-209.

Kurutz, S. (2020). Anders Ericsson, Psychologist and ‘Expert on Experts, Dies at 72, The New York Times, July 2, 2020.

Lasker E., ‘Lasker’s Manual of Chess’. Russell Enterprises 2010. Milford CT USA, pp. 182-184.

McArdle, J. J., Ferrer-Caja, E., Hamagami, F. & Woodcock, R. W. (2002). Comparative longitudinal structural analyses of the growth and decline of multiple intellectual abilities over the life span. Developmental Psychology, 38, 115-142.

R Core Team (2021). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

van Rij, J, (2015a). Visualization of nonlinear interactions.

van Rij, J, (2015b). Overview GAMM analysis of time series data.

J van Rij, N Vaci, LH Wurm, LB Feldman. Alternative quantitative methods in psycholinguistics:

Implications for theory and design. ‘Word Knowledge and Word Usage: a Cross-disciplinary Guide to the Mental Lexicon’, edited by Vito Pirrelli, Ingo Plag, and Wolfgang U. Dressler, Chapter 3. (2018)

van Rij J, Wieling M, Baayen R, van Rijn H (2017). "itsadug: Interpreting Time Series and Autocorrelated Data Using GAMMs." R package version 2.3.

Spillner, V. / Wiesend, B. (2019). (Why) are men better chess players than women? ChessBase News.

Vaci, N., Gula, B., & Bilalić, M. (2014). Restricting range restricts conclusions. Frontiers in Psychology, 5, 569.

Vaci, N., Gula, B., & Bilali, M. (2015). Is Age Really Cruel to Experts? Compensatory Effects of Activity. Psychology and Aging, 30, 740-754.

Vaci, N. , Bilalić´ M. (2017). Chess databases as a research vehicle in psychology: Modeling large data. Behav. Res. Methods 49, 1227–1240.

Vaci, N., Edelsbrunner, P., Stern, E., Neubauer, A.C., Bilalić´, M., & Grabner, R.H. (2019). The Joint Influence of Intelligence and Practice on Skill Development Throughout the Lifespan. Proc Natl Acad Sci USA 116 (37):18363-18369.

Wiesend, B., Researching Age-Related Decline, ChessBase News, 2020.

Winter, B., (2013). Linear models and linear mixed effects models in R with linguistic applications.

Wood, S.N. (2017) Generalized Additive Models: An Introduction with R. Chapman and Hall/CRC.