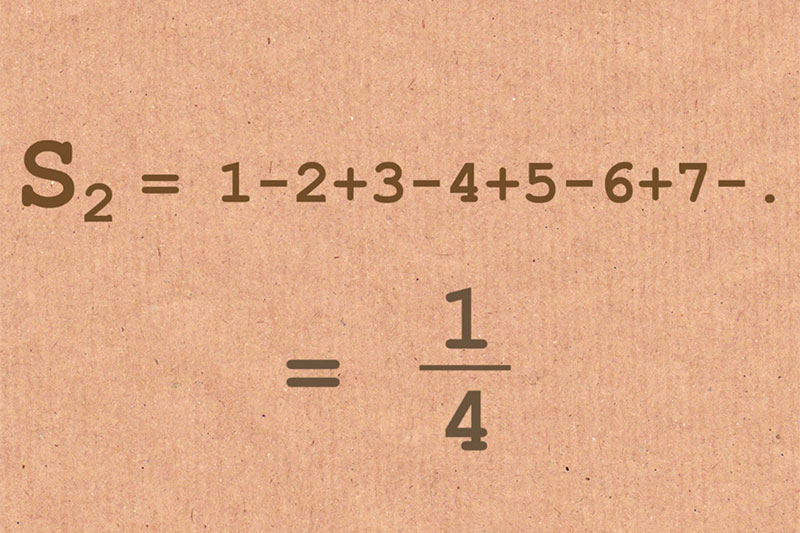
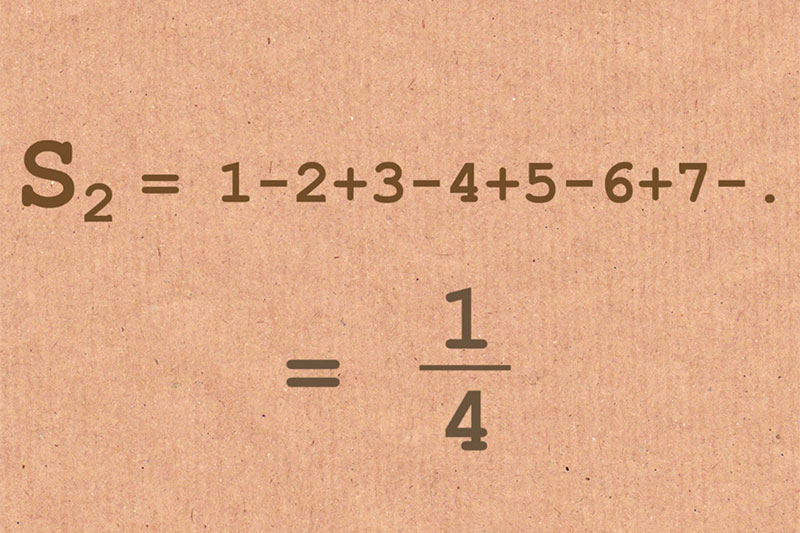
Ever been bored between two chess games? Well, how about calculating a few huge sums. One can for example identify every chessboard square with one number, such as a1 with 1, a2 with 2 … b1 with 9 etc. Then let's sum them all up. If we do it correctly, the sum 1+2+3...+64 will yield 2080.
The nine year old math genius Carl Friedrich Gauß, who was to become one of the most famous mathmaticians of all times, had to do a similar problem once in school. The class was asked by the teacher to add up all numbers to 100. Gauß only needed a minute to come up with the correct answer. His trick: pair up 100 with 1, then 99 with 2 and so forth, and you will receive 50 packages of equal size, namely 101. 50*101=5050. Doesn't make me want to switch places with his teacher.
In fact, this is an instance of a general formula. If one adds up n natural numbers, the sum will always yield n*(n+1)/2, such as for n=100: 100*101/2=50*101=5050.
So if anyone is enthusiastic about this and the break between two chess games long enough: give n a go! It sure will seem as if with increasing n, this product should get ever larger. But does it?
Above: Carl Friedrich Gauß portrait published in Astronomische Nachrichten 1828
Not if modern mathematics is right!
In fact, one can show that the sum of infinitely many natural numbers is not infinite, but can be set equal to -1/12! So 1+2+3+4 … = -1/12. This is not a joke, but rather based on the mathematical theory of analytical continuation.
Two mathmaticians of the Numberphile-Youtube-Channel hosted by Brady Haran show why this is true:
The entire theory is based on ideas by Bernhard Riemann (19th century) und Leonhard Euler (18th century). Both were frustrated with the fact that some sums simply seem to yield infinity, and this escapes our understanding and stops us from learning anything about such sums. The sums in some way act "not well behaved", as mathmaticians put it. This needed to be changed.
So Riemann and Euler looked at certain sums, which were well behaved in some areas but not in others. In fact, they then found a way to somehow transfer the good behavior into the badly behaving areas.
Bernhard Riemann in 1863 and Leonhard Euler (date unknown)
One such sum is the so called Riemann Zeta-Function. It is defined as the sum 1 + 1 / 2^s + 1 / 3^s + ..... . s is a so called complex number.
This sum has well-behaved areas, such as at s=2. If you add all inverse squares 1+1/2^2+1/3^2 … it can be shown that the sum converges towards pi^2/6. This may seem a surprising value, yet it is finite and thus the sum is well-behaved there.
But there is a problem for s=-1. For this, we find
1+1/2^(-1)+1/3^(-2)+.... = 1+2+3+ … which is just the sum of all natural numbers which caused us a head ache due to its seeming divergency towards infinity.
The trick: The Zeta-Function can be written as a very complicated looking mathematical function:
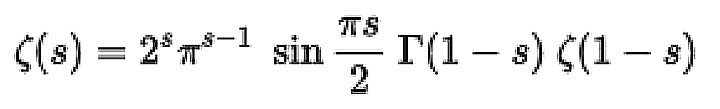
If one now assumes that this function, which is so well behaved for certain s, can be — somehow — also anayltically evaluated in "bad" values of s, then one can simply insert s=-1 into the formula and arrive at: -1/12.
This trick is not only mathematically sound and can be explained much better than by this short article. It also is useful in physics! For example, the sum 1 + 2 + 3 + .... appears in vacuum physics when calculating the force between two plates — the so called Casimir force. There, the minus in front of 1/12 even predicts an attraction, which can be observed. So it's much more than just a mathematical game.
We hope, that nobody has a break between two chess games which is long and boring enough to actually reach -1/12. But then, maybe some of you are interested to learn more about number theory. To those brave readers: dare to use the break between games to visit the really great youtube channel "Numberphile" and enjoy.
Correction October 4: The general formula given in the third paragraph is n(n+1)/2 not over s.
