Chess skill rests on both innate talent and extensive practice and has a lengthy learning curve. Native potential needs much practice to develop fully and talent limits ultimate performance level. However, few FIDE-rated players actually may practice up to their performance limit and much great potential therefore may go unrealized. But exactly how much? How many players "coulda" have achieved "greatness", say have won the grandmaster title, by persisting much further than they did?

Of course, the answer to the question above is "a lot". Other concerns may beckon, motivation to practice may be lax, and for most players the game has modest pay compared to say, tennis.

But to frame the question much more narrowly, what proportion of players who go only some distance in the domain, say who play at least 100 FIDE-rated games without winning the grandmaster title, could have won the title by persevering much longer than they did?  Was it most players, 50%, or just a tiny percentage?

The extent of such unrealized great potential can be very roughly estimated with a simple learning curve mathematical model, an equation which predicts future rating trajectories (see below). Manufacturers and trainers use learning curve models extensively to predict future performance.  Most FIDE-rated players play far too few rated games to win the grandmaster title but a model can estimate what percentage might have done so by persisting much further. The model can approximately predict the average grandmaster trajectory from as few as 100 rated games, as explained below, and then can estimate the percentage of non-grandmasters playing at least 100 games who actually were on that grandmaster trajectory.

The sample

This study’s sample is almost all players entering the FIDE rating list from July 1985, when FIDE first reports game numbers, up to and including the July 1999 list. I eliminated all 198 Myanmar players entering in 1998 and 1999. Some had gained dubious high ratings from controversial tournaments. This left 27,362 players, mostly males (92.73%). These players already were highly selected, males for much of this period needing a minimum 2200 rating for list entry, and later a minimum 2000.

Ratings were examined up to and including the June 2022 list, giving all players at least a 20 year forward span to make their mark.

Key grandmaster parameters

First, I calculated some needed key grandmaster parameters and tested the accuracy of a prediction equation. By June 2022, 822/27,362 (about 3%) had won the grandmaster title, taking a median 472 FIDE-rated games to do so (the range was 30 to 2,291 games).  All but six of the 822 had won the title by 1500 rated games, and so 1500 games was designated as the limit beyond a title win was very unlikely for any player.

Figure 1 presents the mean grandmaster rating trajectory for the 312/822 grandmasters who played at least 1500 games. The ratings are given in 50 game categories using each player’s last rating in each category. 

Figure 1

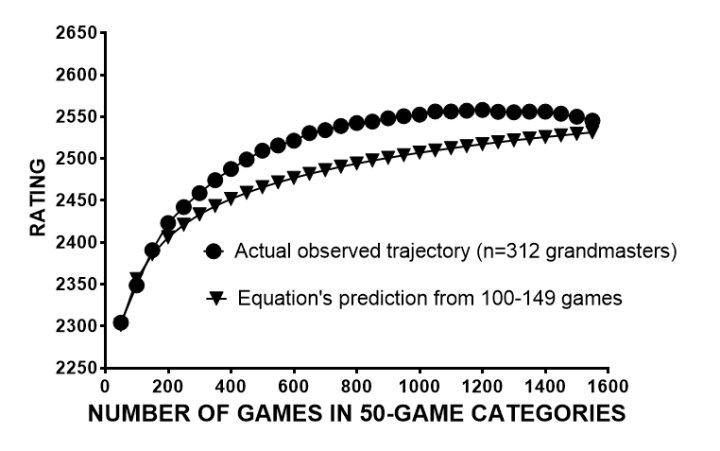
The equation then predicted the mean grandmaster trajectory from three data points (last rating in 0-49, 50-99, and 100-149 games) up to 1500-1549 games.  How well did it work? Figure 1 shows that the equation under-predicts for most data points but is nearly on target by 1500 games, but only on average.  With individual trajectories, the equation had variable success, predicting some much better than others. Nevertheless, the model can roughly estimate what percentage of the sample’s non-grandmasters were on this grandmaster trajectory and had only needed to play more games.

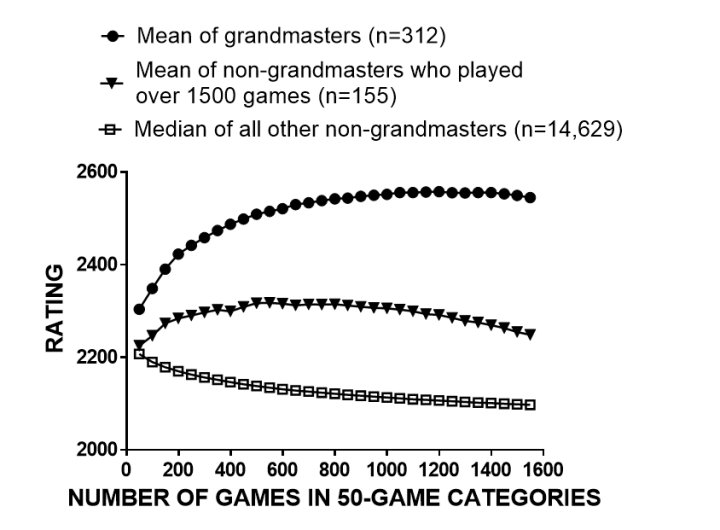
As noted, only six grandmasters had not won the title by 1500 games. Was playing 1500 games alone enough for almost all players to secure the grandmaster title? No, but it seems pretty close at first sight. Of all 977/27,362 players persisting to 1500 games, 66.81% gained the grandmaster title and 70.97% of the remaining 155 won the international master title.

Figure 2 shows the mean rating trajectory for these 155 non-grandmasters. The curve starts lower than the grandmaster curve, peaks earlier and then declines. On average, these players were not on the grandmaster trajectory, so it is not enough for almost anyone just to play 1500 games.

Figure 2

The extent of unfulfilled great potential

The 822 grandmasters took a median 472 rated games to win the title and the median total for all 27,362 players was far less at only 130 games, with 61.59% of the 27,362 playing fewer than 200 games.

Now, playing at least 100 games was designated the minimum for a useful trajectory prediction so only those playing at least 100 but less than 1500 games without winning the grandmaster title were studied, a total of

14,629 players. What percentage were on the grandmaster trajectory, and might have won the grandmaster title by playing 1500 games?

The equation was fitted to each player’s rating data to as many games as they played and then predicted the remaining ratings to 1549 games. So, say a player played 149 games. The model was fitted to three data points and then predicted the remaining data points to 1549 games. Say another played 249 games. The model was fitted to five data points and predicted out to 1549 games. All data were averaged to create a composite curve.

Figure 2 presents the composite curve with median ratings, because some predictions were unrealistically low. The median curve is far from the grandmaster trajectory, actually declining rather than rising.  On average, most players were not on the grandmaster path.

I then calculated peak ratings (the higher of the actual or model-predicted peak rating for each player) and deemed that he or she might have won the grandmaster title by reaching a very lenient 2450 peak. For all 14,629 players, only about 8.30% did so. Some players were too old at list entry to have a realistic chance of winning the title and for the 8,938 players entering the rating list aged under 30 years (their median entry age was 22.08 years), the value was slightly higher at 12.03%.  For the 155 non-grandmasters playing at least 1500 games, only 38.71% achieved a peak rating over 2450.

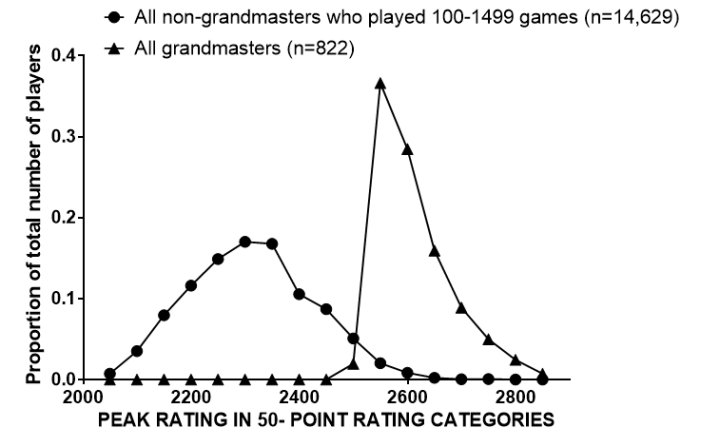
Figure 3 shows the distribution of peak ratings for all grandmasters and the larger of actual or predicted peak rating for non-grandmasters playing between 100 and 1499 games. The distributions overlap very little, again showing that most players were not grandmaster material. The distribution for non-grandmasters was very similar when including only players aged under 30 years at list entry.

Figure 3

Sex differences in unfulfilled potential

How much female great potential in this sample went unrealized? Was it about the same percentage as for the males?

Biological sex differences is the most likely explanation for the male predominance in chess. There are other explanations, such as many fewer females playing (the "participation rate hypothesis") and such social factors as "stereotype threat" and females perceiving a less welcoming, male-oriented chess environment.  But some studies supporting the apparent effects of such factors have grave weaknesses, documented well by Bruno Wiesend.

A quite curious recent study by Sophie Arnold and others asked 286 parents and chess mentors of 654 young players about their potential. The authors concluded that "... the most important adults in young chess players’ lives—their parents and mentors—think that female youth players have less potential than male youth players". Their implication seemed to be that this parental and mentor ‘bias" was short-changing females and discouraging them from persisting. They otherwise would perform as well as males. But perhaps the parents and mentors just saw reality accurately; that females on average do have less innate potential, as with baseball and heavyweight boxing.  Sports coaches and scouts must judge potential well to stay employed. In Northeast Asia, parents may choose their off-springs’ careers (welder, nurse, quantum physicist), the rationale being that they best know each child’s abilities and propensities.

We can see whether just as much female potential went unrealized in the present sample. Females on average play many fewer games and tend to drop out earlier. Indeed, for the 27,362 players, the median games total by June 2022 for males was 133 and 88.5 for females. But for the non-grandmasters who played between 100 and 1499 games, the female median total actually was slightly higher (273 versus 263 games).     

But alas, these females apparently had less great potential on average. Women constituted 7.27% of the 27,362 players but only 2.31% of the 822 grandmasters and a disproportionate 14.84% (23 players) of the 155 non-grandmasters playing over 1500 games. The latter 23 females, playing an astronomical 1500+ games, evidently were not unduly perturbed by any stereotype threats or unwelcoming chess environments.  Indeed, 18/23 won the international master title.

Figure 4 presents the equation-predicted median rating trajectories from at least 100-149 games for males and females. The female curve starts lower and declines slightly but not by as much as the male curve.

Figure 4

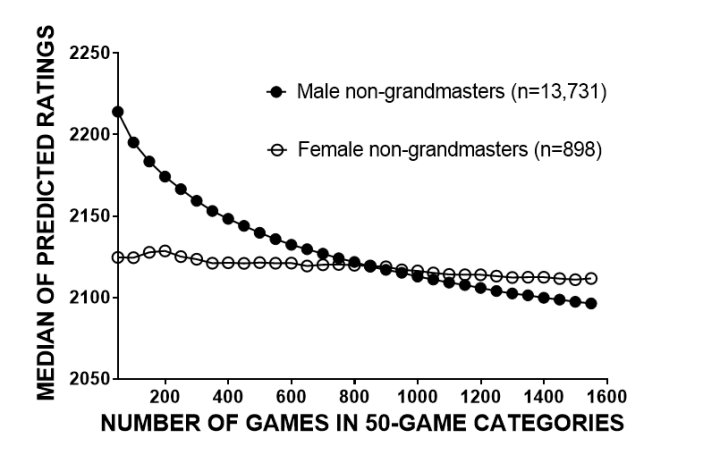
Figure 5 presents the male and female peak rating distributions. They overlap closely but the male distribution has a higher mean and is shifted further to the right. Of the 898 females, only about 3.56% had a predicted or actual peak rating over 2450, versus about 8.61% of the males.

Figure 5

Conclusion

The prediction method is statistical and very rough but the data suggest that most players never would have achieved the grandmaster title by persisting to 1500 games.  Even with the lax criterion of a 2450 peak rating and tacking on a few more percentage points, perhaps only 15% might have done so. Still, that is nearly 2200 players, close to the overall grandmaster total since FIDE made the title official in 1950. As noted, the present sample is highly selected and presumably highly talented. It is uncertain how far the typical club player could go by playing 1500 games. That is another study.

In most real-world domains, great success usually depends very heavily on family background, connections, networking, social skills, luck and widely- varying opportunity. Great talent often does not get a look- in and much immense native potential is wasted. But chess is a meritocracy. Great talent can quickly rise, skill level cannot be faked (barring computer-aided cheating), and chess lacks the equivalent of weak affirmative action hires sailing upwards past the highly talented. Nevertheless, many players may not persist because they gauge accurately that they lack the innate potential to go very far. Such perception is very healthy. The New Age mantra that we can be whatever we want to be does not hold up in chess and players should know their limits.

The prediction equation

The prediction equation is a simple power function, with variants used extensively in manufacturing and training. It predicted the grandmaster trajectory better on average from two other models I tested. The equation is:

Y = 3000 - a P ^b

Where Y is rating, P is the number of games at the end of each 50-game categories (49, 99, 149, etc.), a and b are parameters calculated separately for each player for as many games as they actually played (e.g. 149, 599, up to 1499), and 3000 is the maximum asymptotic rating. The model then predicted their ratings to 1549 games.

Bibliography

Arnold, S. H., Bailey, A. H., Wei, J. M., Shahade, J., and Cimpian, A. (2024). Checking gender bias: Parents and mentors perceive less chess potential in girls. Journal of Experimental Psychology: General, 153, 1-14.

Howard, R.W. (2020). Mapping the outer reaches of the learning curve: Complex intellectual skill performance after decades of extensive practice. Acta Psychologica, 209, 103-135.

Howard, R. W. (2023). Gauging the power of perseverance and extent of unfulfilled potential in one intellectual domain. American Journal of Psychology, 136, 257-271. 

Wiesend, B. (2019). Questioning gender studies on chess. Chessbase.

(https://en.chessbase.com/post/why‑are‑men‑better‑chess‑players‑than‑women)