What was the strongest tournament of all time?

By Jeff Sonas

As with most of the "greatest-ever" debates, there are many ways to answer this question. The simplest answer is to compare the average FIDE rating of the participants in each tournament. That is how a tournament's "Category" is calculated, with 25-point intervals. Thus if the average rating is 2751-2775 it's a "Category 21" tournament; if the average rating is 2726-2750, it's a "Category 20" tournament, and so on.

The 2009 Tal Memorial in Moscow, recently won by Vladimir Kramnik, was a Category 21 tournament, and I don't believe there has ever been a Category 22 tournament. Thus by this approach, the 2009 Tal Memorial would be in a tie for the strongest tournament of all time. However, I do not place much emphasis on "Category" as a measure of tournament strength, mostly because of the large amount of rating inflation that has taken place in the past 25 years. Recent tournaments will look unusually strong by this measure. There must be a more sophisticated way to measure tournament strength.

There is also the problem that official FIDE ratings have only been around since about 1970, yet there were important chess tournaments going back more than a century before then. You can't calculate the strength of a tournament if there are no ratings available! But fortunately we do have the Chessmetrics historical ratings that provide month-by-month ratings from January 2005 all the way back to January of 1843. I haven't calculated new Chessmetrics ratings since January 2005, so for this current analysis, I just used FIDE ratings for the period from January 2005 to the present.

Nevertheless, in order to really assess which were the "strongest" tournaments of all time, you need a method that is completely immune to the effects of rating inflation. Thus I have decided to avoid using ratings directly, and instead to use players' world rankings (e.g. #1 in the world, #7 in the world, etc.) at the time they played in the tournament. This should hopefully eliminate any problems caused by rating inflation.

Ten years ago I developed a simple trick for calculating a Category-like number, using just the world rankings (not ratings) of top ten players in a tournament. I called this alternate number the tournament's "Class", and it was designed to be in the same magnitude as Category (at least for what Category meant ten years ago). Here is the calculation:

A tournament gets 4 points for each participant ranked #1 or #2 in the world.
A tournament gets 3 points for each participant ranked #3 or #4 in the world.
A tournament gets 2 points for each participant ranked #5 or #6 in the world.
A tournament gets 1 point for each participant ranked #7, #8, #9, or #10.

Thus the theoretical maximum, if a tournament included all ten players in the top-ten, would be a Class of 22. There has never been a Class 22 tournament; the ten all-time strongest tournaments by this measure have ranged from Class 19 through Class 21:

	Tournament	Class	Top-10 Participation	Missing Top-10 Player(s)
#1	Vienna, 1882	21	#1, #2, #3, #4, #5, #6, #7, #8, #10	#9 S.Rosenthal
#2	Linares, 1993	21	#1, #2, #3, #4, #5, #6, #7, #8, #10	#9 N.Short
#3	Nottingham, 1936	20	#1, #2, #3, #4, #5, #6, #7, #8	#9 A.Lilienthal #10 P.Keres
#4	AVRO, 1938	20	#1, #2, #3, #4, #5, #6, #7, #8	#9 E.Eliskases #10 V.Pirc
#5	Linares, 1992	20	#1, #2, #3, #4, #5, #6, #7, #8	#9 M.Gurevich #10 A.Shirov
#6	Wijk aan Zee 2001	20	#1, #2, #3, #4, #5, #6, #7, #8	#9 E.Bareev #10 B.Gelfand
#7	London, 1883	19	#1, #2, #3, #4, #5, #6, #7	#8 L.Paulsen #9 V.Hruby #10 A.Wittek
#8	Wijk aan Zee 1999	19	#1, #2, #3, #4, #5, #6, #7	#8 M.Adams #9 A.Karpov #10 N.Short
#9	Linares, 1994	19	#1, #2, #3, #4, #5, #7, #8, #9	#6 V.Salov #10 N.Short
#10	Hastings, 1895	19	#1, #2, #3, #4, #6, #7, #8, #9	#5 P.Lipke #10 J.Showalter

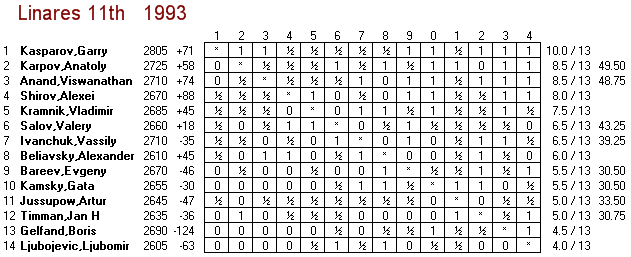
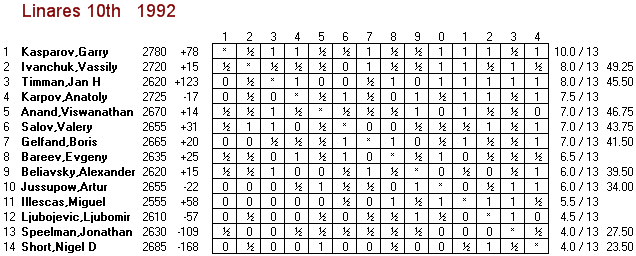
As you can see, there have been six tournaments that had the eight top players in the world, and two of those also had the #10 player (but not the #9 player). Thus the two highest-Class tournaments of all time were Vienna 1882 and Linares 1993, both Class 21. As a tiebreaker, I would give the nod to Vienna 1882 because it also included World Champion Wilhelm Steinitz, who was inactive on the rating list (having not played in six years) and thus not a member of the top ten.

I have previously used the Class calculation to identify the "super-tournaments" throughout chess history, referring to any tournament having a Class of 15 or better. There have been 57 such tournaments, including seven during the current decade (2000 through 2009). The only decade having more super-tournaments was the previous decade (1990 through 1999), which had thirteen. Here are those seven tournaments from the current decade (2000 through 2009):

	Tournament	Class	Top-10 Participation
#6	Wijk aan Zee, 2001	20	#1, #2, #3, #4, #5, #6, #7, #8
#25	Corus A, 2005	17	#2, #3, #4, #5, #6, #7, #8, #9
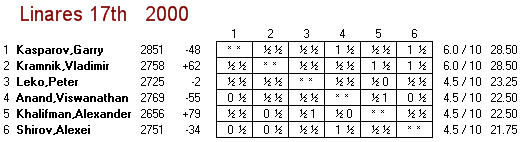
#27	Linares, 2000	16	#1, #2, #3, #4, #5
#29	Corus A, 2008	16	#1, #2, #3, #6, #8, #9, #10
#35	Tal Memorial, 2009	16	#2, #3, #4, #5, #7, #8, #9, #10
#39	Linares, 2005	15	#1, #2, #3, #5, #6
#41	Wijk aan Zee, 2000	15	#1, #2, #3, #5, #7, #9

However, this is not the end of the story. The above approach places the most emphasis on how many top-ten players participated in a tournament, especially top-six players, but there is no penalty if the tournament includes one or more lower-rated players. In fact, from that list of the ten tournaments from history having Class 19+, all but one of them (AVRO 1938) included at least one participant who wasn't even ranked in the top-50 in the world. This is a real problem with the above methodology, since I think a lot of people mean "most elite" when they are talking about the "strongest" tournaments.

So, how can we measure the "most elite" tournament, using only world rank and not directly using ratings? I would say that however many players a tournament has, if they are all taken exactly from the top of the rating list, then it is a perfectly elite tournament. And it should be possible to come up with a formula to measure how close each tournament came to being perfectly elite.

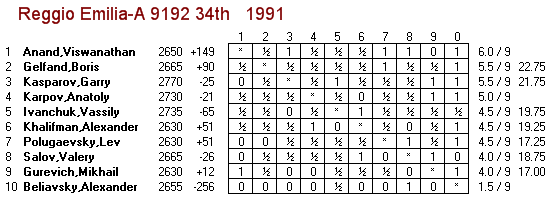
Las Palmas 1996 is frequently cited as being the most elite tournament of all time, supposedly including the top six players and nobody else. However, this does not appear to be true. From the July 1996 FIDE rating list, we find that Vassily Ivanchuk (lowest-rated of the six players at Las Palmas) was #7 on the rating list, with Gata Kamsky (who did not play at Las Palmas) 15 points ahead of him at #6. Perhaps the "live FIDE ratings" at the time would have had Ivanchuk higher up and Kamsky down at #7, but of course those are not available and we wouldn't want to use them even if they were.

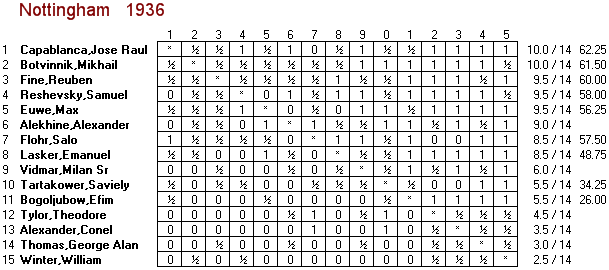
Similarly, my Chessmetrics historical ratings for 01-Dec-1996 (right before the tournament) also have Kamsky at #6 on the list, half a rating point ahead of #7-ranked Las Palmas participant Veselin Topalov. So it turns out the Las Palmas 1996 was not perfectly elite. Very very close, but not quite. The only tournament in history that was perfectly elite was AVRO 1938, which had the top eight players from the 01-Nov-1938 Chessmetrics rating list, and nobody else in the tournament.

To continue this analysis, let's look at the recent ten-player Tal Memorial tournament. An "ideal" ten-player tournament would have players ranked #1, #2, #3, …, #9, #10. If you add up those ranks, you get 1+2+3+…+9+10=55. Instead, the Tal Memorial included #12 and #13, and did not include #1 or #6. So for that tournament, when you add up the ranks, you get 2+3+4+…+10+12+13=73. Dividing 55 by 73 gives 0.75, and by my simple formula, that tells us the tournament was "75% of ideal".

We can do this for all the tournaments in history, and unsurprisingly we find AVRO 1938 on the top of the list, and Las Palmas 1996 at #2 on the list. You may find a few surprises lower down. And it turns out that the recent Tal Memorial shows up as the seventh-most-elite tournament of all time, and the most elite tournament in more than ten years.

	Tournament	%ideal	players	"Non-ideal" participant(s)	"Ideal" player(s) missing
#1	AVRO, 1938	100%	8	(none)	(none)
#2	Las Palmas, 1996	95%	6	#7 V.Topalov	#6 G.Kamsky
#3	Linares, 1998	85%	7	#10 P.Svidler	#5 A.Karpov
#4	Zurich Candidates 1953	83%	15	#16 M.Euwe #25 Y.Averbakh	#2 M.Botvinnik #15 A.Tolush
#5	Reggio Emilia, 1991	80%	10	#11 A.Beliavsky #12 A.Khalifman #15 L.Polugaevsky	#6 N.Short #8 E.Bareev #10 A.Jussupow
#6	St. Petersburg 1895	77%	4	#5 H.Pillsbury	#2 S.Tarrasch
#7	Tal Memorial, 2009	75%	10	#12 V.Ivanchuk #13 R.Ponomariov	#1 V.Topalov #6 V.Gashimov
#8	Linares, 1999	75%	8	#17 P.Leko	#5 A.Shirov
#9	Dortmund, 2001	64%	6	#7 M.Adams #12 V.Topalov	#1 G.Kasparov #6 V.Ivanchuk
#10	Budapest Candidates 1950	61%	10	#11 L.Szabo #19 A.Lilienthal #20 S.Flohr	#1 M.Botvinnik #6 R.Fine #8 S.Reshevsky
#11	Corus A, 2008	60%	14	#15 M.Adams #22 J.Polgar #27 P.Eljanov #36 L.van Wely	#4 A.Morozevich #5 P.Svidler #7 A.Shirov #14 S.Karjakin
#12	Bilbao, 2008	60%	6	#7 T.Radjabov #12 L.Aronian	#2 V.Kramnik #3 A.Morozevich

This is certainly an interesting list, and indicates the historical significance of the 2009 Tal Memorial. You will notice that out of all events that lacked the top-ranked player in the world, it qualifies as the most "elite" tournament ever, since it brought together 10 of the next 12 players below #1 Veselin Topalov, with no participants worse than #13 in the world.

Normally you might think it would be one of the first five FIDE World Championship Candidates Final tournaments (1950 through 1962) that would qualify for the odd distinction as the "most-elite" tournament that also lacked the top-ranked player in the world. In fact, while the 1950 Budapest tournament did indeed attempt to bring together the next ten players after top-rated Mikhail Botvinnik, you can see from the above table that more top-ten-players were omitted than in the recent Tal Memorial, and Budapest also included two participants well below #13 in the world, so on both counts the Tal Memorial seems to have been more elite. And my historical ratings did not consider World Champion Botvinnik to be the top-rated player in the world at the time of the 1953, 1956, 1959, or 1962 Candidates Finals, so in fact each of those tournament did include the top-ranked player in the world (S.Reshevsky in 1953, V.Smyslov in 1956, M.Tal in 1959, and T.Petrosian in 1962) according to Chessmetrics.

In any event, one could legitimately argue that it is a serious omission for an "elite" tournament to be lacking the very top player in the world. It is true that my simple formula would penalize a tournament as much for including the #19 player instead of the #9 player, as it would for including the #11 player instead of the #1 player, and that probably isn't quite right. Instead of a pattern like 1+2+3+…+9+10, we could use the reciprocal of the world rank, and thus it would be 1.00+0.50+0.33+0.25…+0.11+0.10 instead. This rewards the events more that have full participation from the top handful from the rating list, and at the other end it doesn't care as much whether you have #20 or #30. This modification brings Las Palmas 1996 even closer to the "ideal" AVRO 1938. By this final measure, here are the 12 most "elite" tournaments of all time:

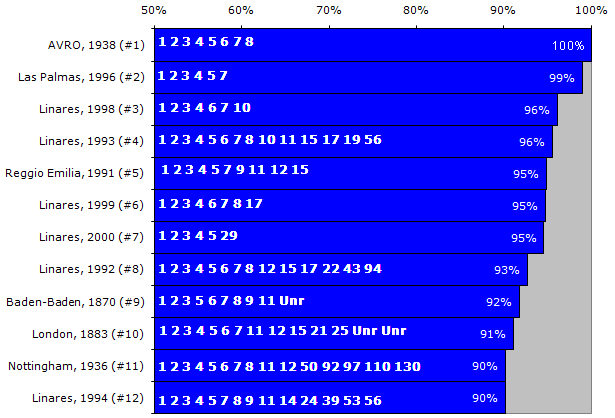
Clearly it would be very hard to argue with the choice of AVRO, 1938 as the strongest, most elite tournament of all time, the perfect blend of top-ten participation and elite selectivity. After that tournament, it's not as clear; it really depends on whether you think a "strong" tournament means it has a host of top-ten players, or if you mean it is an extremely elite event. It is difficult for one tournament to accomplish provide both. Either way, the above data should hopefully be a good resource for the next time you want to argue about what was the strongest tournament of all time!

Copyright Chessmetrics

Cross tables of the twelve top tournaments

Looking back in nostalgia

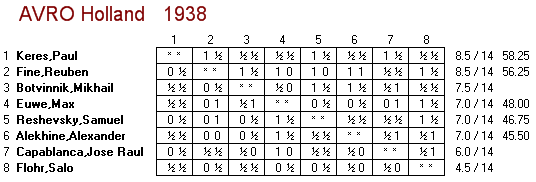
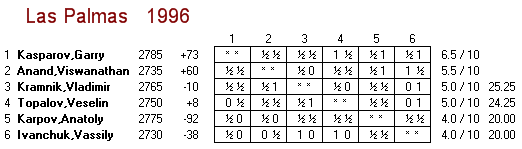
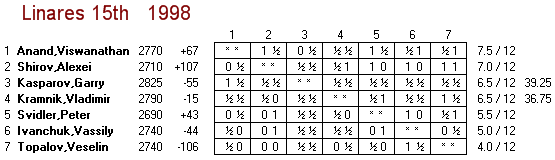
In 1996, with the Las Palmas tournament completed, the fledgling ChessBase news page, set up with the assistance of John Nunn, was up and running. The Wayback Machine has archived the front page from December 18 (but not all the links), and this is what it looked like:

As you can see we had a report on the second strongest tournament of all time, with blinking headline and all. Unfortunately the report itself is gone, although you can still see it, with pictures and videos, on an ancient CD of ChessBase Magazine. Click around the above page for other fun bits – and no, we are not taking orders for Fritz 4 or ChessBase 6 any more.